题目内容
已知二次函数y=f(x)满足f(0)=f(1)=1,且f(
)=
,求:
(Ⅰ)f(x)的解析式;
(Ⅱ)f(x)在(0,1)上的值域.
| 1 |
| 2 |
| 3 |
| 4 |
(Ⅰ)f(x)的解析式;
(Ⅱ)f(x)在(0,1)上的值域.
考点:二次函数的性质
专题:函数的性质及应用
分析:(I)设f(x)的一般式y=ax2+bx+c,结合f(0)=f(1)=1,且f(
)=
,分别代入得到关于a、b、c的方程组,然后解方程组即可.
(II)结合(I)中函数的解析式和二次函数的图象和性质,分析函数的最值,进而可得f(x)在(0,1)上的值域
| 1 |
| 2 |
| 3 |
| 4 |
(II)结合(I)中函数的解析式和二次函数的图象和性质,分析函数的最值,进而可得f(x)在(0,1)上的值域
解答:
解:(Ⅰ)设f(x)的一般式y=ax2+bx+c,
∵f(0)=f(1)=1,且f(
)=
,
∴
解得
∴f(x)=x2-x+1…..…(6分)
(Ⅱ)f(x)=x2-x+1的解析式可化为:
f(x)=(x-
)2+
,x∈(0,1);
当x=
时,f(x)min=
;当x=1时,f(1)=1,
综上,f(x)在(0,1)上的值域是[
,1)…(13分)
∵f(0)=f(1)=1,且f(
| 1 |
| 2 |
| 3 |
| 4 |
∴
|
解得
|
∴f(x)=x2-x+1…..…(6分)
(Ⅱ)f(x)=x2-x+1的解析式可化为:
f(x)=(x-
| 1 |
| 2 |
| 3 |
| 4 |
当x=
| 1 |
| 2 |
| 3 |
| 4 |
综上,f(x)在(0,1)上的值域是[
| 3 |
| 4 |
点评:本题考查的知识点是二次函数的图象和性质,二次函数解析式的求法,熟练掌握待定系数法的步骤和二次函数的图象和性质是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

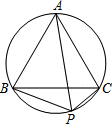 如图,P是等边△ABC外接圆
如图,P是等边△ABC外接圆