ΧβΡΩΡΎ»ί
“―÷Σ≈ΉΈοœΏx=
y2ΒΡΫΙΒψ”κΆ÷‘≤CΘΚ
+
=1Θ®aΘΨbΘΨ0Θ©ΒΡ“ΜΗωΫΙΒψ÷ΊΚœΘ§F1ΓΔF2 «Ά÷‘≤CΒΡΉσΓΔ”“ΫΙΒψΘ§Q «Ά÷‘≤C…œ»Έ“β“ΜΒψΘ§«“
•
ΒΡΉν¥σ÷Β «3Θ°
Θ®ΔώΘ©«σΆ÷‘≤CΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®ΔρΘ©Ιΐ”“ΫΙΒψF2Ής–±¬ ΈΣkΒΡ÷±œΏl”κΆ÷‘≤CΫΜ”ΎMΓΔNΝΫΒψΘ§‘Ύx÷α…œ «Ζώ¥φ‘ΎΒψPΘ®mΘ§0Θ©Θ§ ΙΒΟPMΓΔPNΈΣΝΎ±ΏΒΡΤΫ––ΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ωmΒΡ»Γ÷ΒΖΕΈßΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
| 1 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| QF1 |
| QF2 |
Θ®ΔώΘ©«σΆ÷‘≤CΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®ΔρΘ©Ιΐ”“ΫΙΒψF2Ής–±¬ ΈΣkΒΡ÷±œΏl”κΆ÷‘≤CΫΜ”ΎMΓΔNΝΫΒψΘ§‘Ύx÷α…œ «Ζώ¥φ‘ΎΒψPΘ®mΘ§0Θ©Θ§ ΙΒΟPMΓΔPNΈΣΝΎ±ΏΒΡΤΫ––ΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ωmΒΡ»Γ÷ΒΖΕΈßΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΩΦΒψΘΚ÷±œΏ”κ‘≤ΉΕ«ζœΏΒΡΉέΚœΈ Χβ
Ή®ΧβΘΚ‘≤ΉΕ«ζœΏ÷–ΒΡΉν÷Β”κΖΕΈßΈ Χβ
Ζ÷ΈωΘΚΘ®ΔώΘ©”…Χβ“βΆΤΒΦ≥ωΆ÷‘≤CΘΚ
+
=1Θ®aΘΨbΘΨ0Θ©ΒΡΫΙΒψΈΣF1Θ®-1Θ§0Θ©Θ§F2Θ®1Θ§0Θ©Θ§…ηQΘ®xΘ§yΘ©Θ§‘ρ
•
=b2-1+
x2Γήb2-1+c2Θ§”…¥ΥΡή«σ≥ωΆ÷‘≤ΖΫ≥ΧΘ°
Θ®ΔρΘ©”…Χβ“β÷ΣlΘΚy=kΘ®x-1Θ©Θ§ΝΣΝΔ
Θ§ΒΟΘ®3+4k2Θ©x2-8k2x+4k2-12=0Θ§άϊ”ΟΈΛ¥οΕ®άμΫαΚœ“―÷ΣΧθΦΰΆΤΒΦ≥ω¥φ‘Ύ¬ζΉψΧβ“βΒΡΒψP«“Ρή«σ≥ωmΒΡ»Γ÷ΒΖΕΈßΘ°
| x2 |
| a2 |
| y2 |
| b2 |
| QF1 |
| QF2 |
| c2 |
| a2 |
Θ®ΔρΘ©”…Χβ“β÷ΣlΘΚy=kΘ®x-1Θ©Θ§ΝΣΝΔ
|
Ϋβ¥πΘΚ
ΫβΘΚΘ®ΔώΘ©ΓΏ≈ΉΈοœΏx=
y2ΒΡΫΙΒψΉχ±ξΈΣFΘ®1Θ§0Θ©Θ§
Γύ”…Χβ“β÷ΣΆ÷‘≤CΘΚ
+
=1Θ®aΘΨbΘΨ0Θ©ΒΡΫΙΒψΈΣF1Θ®-1Θ§0Θ©Θ§F2Θ®1Θ§0Θ©Θ§
Γύc=1Θ§
…ηQΘ®xΘ§yΘ©Θ§‘ρ
•
=Θ®-1-xΘ§-yΘ©•Θ®1-xΘ§-yΘ©=x2-1+y2
=x2-1+b2(1-
)
=b2-1+
x2Θ§
ΓΏ-aΓήxΓήaΘ§
Γύ
•
=b2-1+
x2Γήb2-1+c2Θ§
Γύb2-1+c2=3Θ§
Γύb2+c2=4=a2Θ§
Γύa2=4Θ§b2=3Θ§
ΓύΆ÷‘≤ΖΫ≥ΧΈΣ
+
=1Θ°
Θ®ΔρΘ©”…Χβ“β÷ΣlΘΚy=kΘ®x-1Θ©Θ§
ΝΣΝΔ
Θ§’ϊάμΘ§ΒΟΘ®3+4k2Θ©x2-8k2x+4k2-12=0Θ§
…ηMΘ®x1Θ§y1Θ©Θ§NΘ®x2Θ§y2Θ©Θ§‘ρx1+x2=
Θ§
y1+y2=kΘ®x1+x2-2Θ©Θ§
+
=Ȯx1-mȧy1ȩ+Ȯx2-mȧy2ȩ
=Ȯx1+x2-2mȧy1+y2ȩȧ
ΓΏΝβ–ΈΒΡΕ‘Ϋ«œΏΜΞœύ¥Ι÷±Θ§ΓύΘ®
+
Θ©•
=0Θ§
ΓύΘ®x1-x2Θ©[x1+x2-2m+kΘ®y1+y2Θ©]=0Θ§
ΓύkΘ®y1+y2Θ©+x1+x2-2m=0Θ§
Γύk2Θ®x1+x2-2Θ©+x1+x2-2m=0Θ§
Γύk2(
-2)+
-2m=0Θ§
”…“―÷ΣΧθΦΰ÷ΣkΓΌ0Θ§«“kΓ RΘ§
Γύm=
=
Θ§Γύ0ΘΦmΘΦ
Θ§
Γύ¥φ‘Ύ¬ζΉψΧβ“βΒΡΒψP«“mΒΡ»Γ÷ΒΖΕΈß «Θ®0Θ§
Θ©Θ°
| 1 |
| 4 |
Γύ”…Χβ“β÷ΣΆ÷‘≤CΘΚ
| x2 |
| a2 |
| y2 |
| b2 |
Γύc=1Θ§
…ηQΘ®xΘ§yΘ©Θ§‘ρ
| QF1 |
| QF2 |
=x2-1+b2(1-
| x2 |
| a2 |
=b2-1+
| c2 |
| a2 |
ΓΏ-aΓήxΓήaΘ§
Γύ
| QF1 |
| QF2 |
| c2 |
| a2 |
Γύb2-1+c2=3Θ§
Γύb2+c2=4=a2Θ§
Γύa2=4Θ§b2=3Θ§
ΓύΆ÷‘≤ΖΫ≥ΧΈΣ
| x2 |
| 4 |
| y2 |
| 3 |
Θ®ΔρΘ©”…Χβ“β÷ΣlΘΚy=kΘ®x-1Θ©Θ§
ΝΣΝΔ
|
…ηMΘ®x1Θ§y1Θ©Θ§NΘ®x2Θ§y2Θ©Θ§‘ρx1+x2=
| 8k2 |
| 3+4k2 |
y1+y2=kΘ®x1+x2-2Θ©Θ§
| PM |
| PN |
=Ȯx1+x2-2mȧy1+y2ȩȧ
ΓΏΝβ–ΈΒΡΕ‘Ϋ«œΏΜΞœύ¥Ι÷±Θ§ΓύΘ®
| PM |
| PN |
| MN |
ΓύΘ®x1-x2Θ©[x1+x2-2m+kΘ®y1+y2Θ©]=0Θ§
ΓύkΘ®y1+y2Θ©+x1+x2-2m=0Θ§
Γύk2Θ®x1+x2-2Θ©+x1+x2-2m=0Θ§
Γύk2(
| 8k2 |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
”…“―÷ΣΧθΦΰ÷ΣkΓΌ0Θ§«“kΓ RΘ§
Γύm=
| k2 |
| 3+4k2 |
| 1 | ||
|
| 1 |
| 4 |
Γύ¥φ‘Ύ¬ζΉψΧβ“βΒΡΒψP«“mΒΡ»Γ÷ΒΖΕΈß «Θ®0Θ§
| 1 |
| 4 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΆ÷‘≤ΒΡ±ξΉΦΖΫ≥ΧΒΡ«σΖ®Θ§ΩΦ≤ι¬ζΉψΧθΦΰΒΡΒψ «Ζώ¥φ‘ΎΒΡ≈–ΕœΘ§ΉέΚœ–‘«ΩΘ§Ρ―Ε»¥σΘ§ΨΏ”–“ΜΕ®ΒΡΧΫΥς–‘Θ§ΫβΧβ ±“ΣΉΔ“βΚ· ΐΖΫ≥ΧΥΦœκΒΡΚœάμ‘Υ”ΟΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
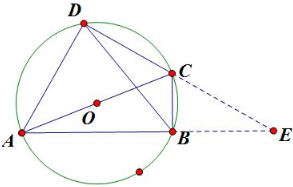
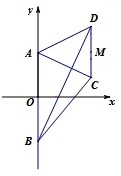 »γΆΦΘ§Χί–ΈABCDΒΡΒΉ±ΏAB‘Ύy÷α…œΘ§‘≠ΒψOΈΣABΒΡ÷–ΒψΘ§|AB|=
»γΆΦΘ§Χί–ΈABCDΒΡΒΉ±ΏAB‘Ύy÷α…œΘ§‘≠ΒψOΈΣABΒΡ÷–ΒψΘ§|AB|=