题目内容
 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求a,b的值;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当
| S |
| |k| |
| 16 |
| 9 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆C:
+
=1(a>b>0)的离心率为
,短轴长是2,结合a2=b2+c2,即可求出a,b的值;
(2)设l1的方程为y=kx-1,代入
+y2=1,求出M的坐标,可得DM,用-
代k得DN,求出△DMN的面积,可得
=
,利用
>
,可得
>
,从而可求k的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(2)设l1的方程为y=kx-1,代入
| x2 |
| 4 |
| 1 |
| k |
| S |
| |k| |
| 32(1+k2) |
| (1+4k2)(4+k2) |
| S |
| |k| |
| 16 |
| 9 |
| 32(1+k2) |
| (1+4k2)(4+k2) |
| 16 |
| 9 |
解答:
解:(1)设椭圆C的半焦距为c,则由题意得
,
又a2=b2+c2,
联立解得a=2,b=1. …(4分)
(2)由(1)知,椭圆C的方程为
+y2=1,所以椭圆C与y轴负半轴交点为D(0,-1).
因为l1的斜率存在,所以设l1的方程为y=kx-1,
代入
+y2=1,得M(
,
),
从而DM=
. …(6分)
用-
代k得DN=
.
所以△DMN的面积S=
?
×
=
. …(8分)
则
=
,
因为
>
,即
>
,
整理得4k4-k2-14<0,解得-
<k2<2
所以0<k2<2,即-
<k<0或0<k<
.
从而k的取值范围为(-
,0)∪(0,
).
|
又a2=b2+c2,
联立解得a=2,b=1. …(4分)
(2)由(1)知,椭圆C的方程为
| x2 |
| 4 |
因为l1的斜率存在,所以设l1的方程为y=kx-1,
代入
| x2 |
| 4 |
| 8k |
| 1+4k2 |
| 4k2-1 |
| 1+4k2 |
从而DM=
8|k|
| ||
| 1+4k2 |
用-
| 1 |
| k |
8
| ||
| 4+k2 |
所以△DMN的面积S=
| 1 |
| 2 |
8|k|
| ||
| 1+4k2 |
8
| ||
| 4+k2 |
| 32(1+k2)|k| |
| (1+4k2)(4+k2) |
则
| S |
| |k| |
| 32(1+k2) |
| (1+4k2)(4+k2) |
因为
| S |
| |k| |
| 16 |
| 9 |
| 32(1+k2) |
| (1+4k2)(4+k2) |
| 16 |
| 9 |
整理得4k4-k2-14<0,解得-
| 7 |
| 4 |
所以0<k2<2,即-
| 2 |
| 2 |
从而k的取值范围为(-
| 2 |
| 2 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查解不等式,考查学生的计算能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知x,y满足
,且z=2x+y的最大值是最小值的4倍,则a的值是( )
|
A、
| ||
B、
| ||
C、
| ||
| D、4 |

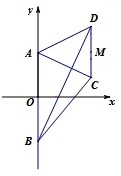 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=