题目内容
10.函数f(x)=(2k-1)x+1在R上单调递减,则k的取值范围是(-∞,$\frac{1}{2}$).分析 根据题意,当2k-1≠0时,函数f(x)=(2k-1)x+1为一次函数,由一次函数的性质分析可得答案.
解答 解:根据题意,当2k-1≠0时,函数f(x)=(2k-1)x+1为一次函数,
若f(x)=(2k-1)x+1在R上单调递减,
则有2k-1<0,解可得k<$\frac{1}{2}$,
即k的取值范围是(-∞,$\frac{1}{2}$);
故答案为:(-∞,$\frac{1}{2}$).
点评 本题考查函数单调性的性质,关键是熟悉常见函数的单调性以及判定方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知集合A={x|x-x2<0},B={0,1,2,3},则(∁RA)∩B=( )
| A. | {0,1} | B. | {x|0≤x≤1} | C. | {2,3} | D. | {1,2,3} |
2.已知动点P在曲线2y2-x=0上移动,则点A(-2,0)与点P连线中点的轨迹方程是( )
| A. | y=2x2 | B. | y=8x2 | C. | x=4y2-1 | D. | y=4x2-$\frac{1}{2}$ |
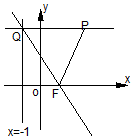 如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.
如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.