题目内容
2.已知动点P在曲线2y2-x=0上移动,则点A(-2,0)与点P连线中点的轨迹方程是( )| A. | y=2x2 | B. | y=8x2 | C. | x=4y2-1 | D. | y=4x2-$\frac{1}{2}$ |
分析 设出点A(-2,0)与点P连线中点的坐标,利用中点坐标公式可得P(2x,2y+1),根据动点P在曲线上移动,代入方程即可求得点A(-2,0)与点P连线中点的轨迹方程
解答 解:设点A(-2,0)与点P连线中点坐标为(x,y),
则由中点坐标公式可得P(2x+2,2y),
∵动点P在曲线2y2-x=0上移动,
∴2(2y)2-(2x+2)=0
即x=4y2-1.
故选:C.
点评 本题考查轨迹方程的求法,考查中点坐标公式,考查代入法的运用,解题的关键是确定动点坐标之间的关系.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.了研究某种细菌在特定环境下随时间变化的繁殖情况,得如下实验数据:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,预测t=8时,细菌繁殖个数.
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
(2)利用(1)中的回归方程,预测t=8时,细菌繁殖个数.
17.某地区2011年至2015年农村居民家庭人均纯收入y(单位:万元)的数据如表:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}•\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}}\\{\hat a=\overline y-\hat b\overline x}\end{array}}\right.$.
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
(2)利用(1)中的回归方程,分析2011年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}•\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}}\\{\hat a=\overline y-\hat b\overline x}\end{array}}\right.$.
7.已知抛物线C:y2=2px(p>0)上一点(5,m)到焦点的距离为6,P,Q分别为抛物线C与圆M:(x-6)2+y2=1上的动点,当|PQ|取得最小值时,向量$\overrightarrow{PQ}$在x轴正方向上的投影为( )
| A. | 2-$\frac{{\sqrt{5}}}{5}$ | B. | 2$\sqrt{5}$-1 | C. | 1-$\frac{{\sqrt{21}}}{21}$ | D. | $\sqrt{21}$-1 |
11.直线x-y+3=0被圆(x+2)2+(y-2)2=1截得的弦长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{6}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
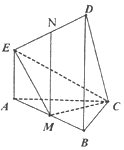 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.