题目内容
1.某单位决定投资3200元建仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价40元,两面墙砌砖,每米造价45元,顶部每平方米造价20元.(1)设铁栅长为x米,一堵砖墙长为y米,求函数y=f(x)的解析式.
(2)为使仓库总面积S达到最大,正面铁栅应设计为多长?并求S的最大值.
分析 (1)长为x米,宽为y米,则40x+90y+20xy=3200,可得函数y=f(x)的解析式;
(2)由40x+90y≥120$\sqrt{xy}$,得$\sqrt{xy}$的取值范围,即S=xy的取值范围;由40x=90y,且xy=100,解得x,y的值即可.
解答 解:(1)由题意,知:40x+2y×45+20xy=3200,
所以$f(x)=\frac{320-4x}{9+2x}(0<x<80)$
(2)因为40x+90y≥120$\sqrt{xy}$(当且仅当40x=90y时取“=”),
所以:3200≥120$\sqrt{xy}$+20xy,
所以,0<$\sqrt{xy}$≤10;
所以,S=xy≤100.
当40x=90y时,S取最大值,又xy=100,
所以x=15,y=$\frac{20}{3}$,
所以,正面铁栅应设计为15米长,S的最大值为100平方米.
点评 本题考查了长方体模型的应用,在求面积S=xy最值时,利用基本不等式是关键.

练习册系列答案
相关题目
9.函数f(x)=cos(x+φ)(0≤φ≤π)的定义域为R,若f(x)为奇函数,则φ=( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
13.了研究某种细菌在特定环境下随时间变化的繁殖情况,得如下实验数据:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,预测t=8时,细菌繁殖个数.
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
(2)利用(1)中的回归方程,预测t=8时,细菌繁殖个数.
11.直线x-y+3=0被圆(x+2)2+(y-2)2=1截得的弦长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{6}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
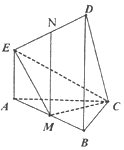 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.