题目内容
已知函数f(x)=|x|+
-1(x≠0).
(1)若对任意x∈R,不等式f(2x)>0恒成立,求m的取值范围;
(2)讨论函数f(x)零点的个数.
| m |
| x |
(1)若对任意x∈R,不等式f(2x)>0恒成立,求m的取值范围;
(2)讨论函数f(x)零点的个数.
考点:函数恒成立问题,函数零点的判定定理
专题:综合题,函数的性质及应用
分析:(1)f(2x)>0恒成立?2x+
-1>0(x≠0)恒成立?m>2x(1-2x)(x≠0)恒成立,构造函数g(x)=2x(1-2x)(x≠0),利用基本不等式(或配方法)可求得m的取值范围;
(2)当x>0时,由f(x)=x+
-1=0得:m=x(1-x)=-(x-
)2+
;同理可得,当x<0时,m=x(1+x)=(x+
)2-
,在在同一直角坐标系中作出函数y=m与函数y=|x|(x-1)的图象,借助图象即可求得函数f(x)零点的个数.
| m |
| 2x |
(2)当x>0时,由f(x)=x+
| m |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:(1)f(2x)>0恒成立?2x+
-1>0(x≠0)恒成立?m>2x(1-2x)(x≠0)恒成立,
令g(x)=2x(1-2x)(x≠0),
则m>g(x)max,
因为g(x)=2x(1-2x)≤(
)2=
(当且仅当x=-1时取“=”),
∴g(x)max=
,
∴m>
;
(2)当x>0时,由f(x)=x+
-1=0得:m=x(1-x)=-(x-
)2+
,
当x<0时,由f(x)=-x+
-1=0得:m=x(1+x)=(x+
)2-
,
在同一直角坐标系中作出函数y=m与函数y=|x|(x-1)的图象,
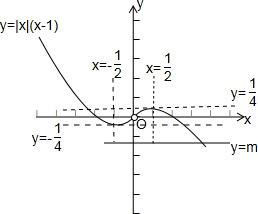
由图象知,当m<-
或m>
时,函数f(x)=|x|+
-1(x≠0)有一个零点;
当m=±
或m=0时,函数f(x)=|x|+
-1(x≠0)有两个零点;
当-
<m<0或0<m<
时,函数f(x)=|x|+
-1(x≠0)有三个零点.
| m |
| 2x |
令g(x)=2x(1-2x)(x≠0),
则m>g(x)max,
因为g(x)=2x(1-2x)≤(
| 2x+(1-2x) |
| 2 |
| 1 |
| 4 |
∴g(x)max=
| 1 |
| 4 |
∴m>
| 1 |
| 4 |
(2)当x>0时,由f(x)=x+
| m |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
当x<0时,由f(x)=-x+
| m |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
在同一直角坐标系中作出函数y=m与函数y=|x|(x-1)的图象,

由图象知,当m<-
| 1 |
| 4 |
| 1 |
| 4 |
| m |
| x |
当m=±
| 1 |
| 4 |
| m |
| x |
当-
| 1 |
| 4 |
| 1 |
| 4 |
| m |
| x |
点评:本题考查函数恒成立问题,考查函数零点的判定定理的应用,作图是关键,也是难点,着重考查等价转化思想与数形结合思想、分类讨论思想的综合运用,属于难题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知等比数列{an}的公比为q,且a1>0,则“q>0”是“数列{an}为递增数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
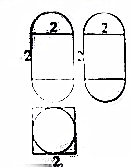 某几何体的三视图如图所示,则该几何体的体积( )
某几何体的三视图如图所示,则该几何体的体积( )A、4+
| ||
B、8+
| ||
C、8+
| ||
D、8+
|
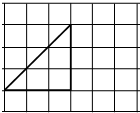
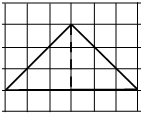
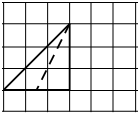
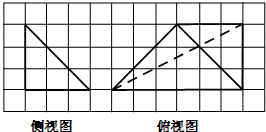 如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )
如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )