Question

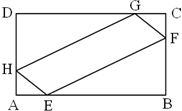如图所示，在矩形ABCD中，已知AB=a，BC=b（a＞b），在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x，当x取何值时，四边形EFGH的面积最大？并求出这个最大面积．

Answer 1

考点：基本不等式在最值问题中的应用

专题：应用题,不等式的解法及应用

分析：先表示出面积，再分类讨论，即可求出四边形EFGH的面积最大．

解答： 解：S△EHA=S△CGF=

1

2

x2（2分）S△BEF=S△DHG=

1

2

(a-x)(b-x)（2分）
∴S_{平行四边形EFGH}=ab-2[

1

2

x2+

1

2

(a-x)(b-x)]=-2x²+（a+b）x（0＜x≤b）（6分）
S=-2(x-

a+b

4

)2+

(a+b)2

8

由0＜x≤b及a＞b＞0得0＜b＜

a+b

2

（ⅰ）若

a+b

4

≤b，即a≤3b时，x=

a+b

4

时S取得最大值

(a+b)2

8

（9分）
（ⅱ）若

a+b

4

＞b，即a＞3b，函数S(x)在(0，b]上是增函数，
 因此，当x=b时，面积S取得最大值ab-b²（13分）
答：（ⅰ）当

a+b

4

≤b，x取

a+b

4

时，四边形EFGH的面积最大，最大值为

(a+b)2

8

（ⅱ）当

a+b

4

＞b，x取b时，四边形EFGH的面积最大，最大值为ab-b2

点评：本题考查利用数学知识解决实际问题，考查分类讨论的数学思想，属于中档题．