题目内容
是否存在锐角α,β,使
+β=
,tan
•tanβ=2-
同时成立?若存在,求出α,β的度数;若不存在,请说明理由.
| α |
| 2 |
| π |
| 3 |
| α |
| 2 |
| 3 |
考点:两角和与差的正切函数
专题:计算题,三角函数的求值
分析:利用条件
+β=
,tan
•tanβ=2-
构造关于tan
、tanβ的方程组,解出tan
、tanβ,进而求出α,β的度数.
| α |
| 2 |
| π |
| 3 |
| α |
| 2 |
| 3 |
| α |
| 2 |
| α |
| 2 |
解答:
解:存在.
∵
=tan
=tan(
+β)=
=
∴tan
+tanβ=3-
…①
tan
•tanβ=2-
…②
由①②解得:
或
∴
(舍),
∴存在α=30°,β=45°满足题意.
∵
| 3 |
| π |
| 3 |
| α |
| 2 |
tan
| ||
1-tan
|
tan
| ||
1-(2-
|
∴tan
| α |
| 2 |
| 3 |
tan
| α |
| 2 |
| 3 |
由①②解得:
|
|
∴
|
|
∴存在α=30°,β=45°满足题意.
点评:解决本题的关键是根据两式同时成立构各造方程组,求解过程中注意α,β为锐角.

练习册系列答案
相关题目
若函数f(x)=logax(a>0且a≠1)经过点(4,2),则f(2)=( )
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
复数z=
,则|z|=( )
| 2 |
| 1+i |
| A、1 | ||
| B、0 | ||
C、
| ||
| D、2 |
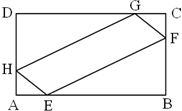 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.
如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.