题目内容
参数方程
(θ为参数)化为普通方程是( )
|
| A、2x-y+1=0 |
| B、2x+y-1=0 |
| C、2x-y+1=0,x∈[0,1] |
| D、2x+y-1=0,x∈[0,1] |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:首先利用三角恒等变换,进一步利用同角三角恒等式求的结果
解答:
解:由于
,
则:2x=2sin2θ①,
y=2cos2θ-1②,
解①②得:2x+y-1=0,
由于0≤sin2θ≤1,
故选:D.
|
则:2x=2sin2θ①,
y=2cos2θ-1②,
解①②得:2x+y-1=0,
由于0≤sin2θ≤1,
故选:D.
点评:本题考查的知识要点:三角函数关系式的变换,参数方程和直角坐标方程的互化.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
复数z=
,则|z|=( )
| 2 |
| 1+i |
| A、1 | ||
| B、0 | ||
C、
| ||
| D、2 |
下列命题中正确的是( )
| A、若a>b,则ac2>bc2 | ||||
B、若a>b,c<d,则
| ||||
| C、若a>b,c>d,则a-c>b-d | ||||
D、若ab>0,a>b,则
|
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( )


| A、7 | ||
B、
| ||
C、
| ||
D、
|
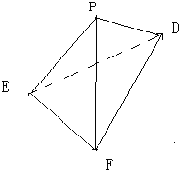 三棱锥P-DEF中,顶点P在平面DEF上的射影为O.
三棱锥P-DEF中,顶点P在平面DEF上的射影为O.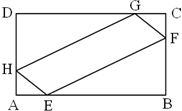 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.
如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.