题目内容
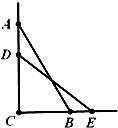 如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,
如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,且AD=(
| 3 |
| 2 |
考点:轨迹方程
专题:
分析:根据直角三角形斜边上的中线等于斜边的一半得到CO=
AB=
DE=CO′,即O运动所经过的路线是一段圆弧;在Rt△ACB中,根据直角三角形三边的关系得到∠ACO=30°,CA=
,则易求出CD=CA-DA=
,即可得到△DCE为等腰直角三角形,得到∠DEC=45°,则∠OCO′=∠DCO′-∠ACO=15°,然后根据弧长公式计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:连接CO、CO′,如图,
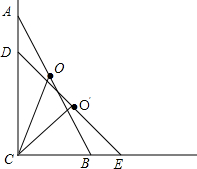
∵CA⊥CB,O为AB中点,O′为DE的中点,
∴CO=
AB=
DE=CO′,
∵AB=2,
∴CO=1,
当A端下滑B端右滑时,AB的中点O到C的距离始终为定长1,
∴O运动所经过的路线是一段圆弧,
∵∠ABC=60°,
∴∠ACO=30°,CA=
,
∵AD=
-
,
CD=CA-AD=
-(
-
)=
,
∴sin∠DEC=
=
,
∴∠DEC=45°,
∴∠DCO′=45°
∴∠OCO′=∠DCO′-∠ACO=15°,
∴弧OO′的长=
=
,
即O点运动到O′所经过路线OO′的长为
.

∵CA⊥CB,O为AB中点,O′为DE的中点,
∴CO=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=2,
∴CO=1,
当A端下滑B端右滑时,AB的中点O到C的距离始终为定长1,
∴O运动所经过的路线是一段圆弧,
∵∠ABC=60°,
∴∠ACO=30°,CA=
| 3 |
∵AD=
| 3 |
| 2 |
CD=CA-AD=
| 3 |
| 3 |
| 2 |
| 2 |
∴sin∠DEC=
| CD |
| DE |
| ||
| 2 |
∴∠DEC=45°,
∴∠DCO′=45°
∴∠OCO′=∠DCO′-∠ACO=15°,
∴弧OO′的长=
| 15π |
| 180 |
| π |
| 12 |
即O点运动到O′所经过路线OO′的长为
| π |
| 12 |
点评:本题考查了动点的运动轨迹问题,解答的关键是明确AB中点在以C为圆心的圆弧上运动,考查了弧长公式及直角三角形中的边角关系,是中档题.

练习册系列答案
相关题目
设f(n)=(
)n-1+(
)n+1(n∈Z),则f(2014)( )
| 1+i |
| 1-i |
| 1-i |
| 1+i |
| A、2 | B、-2 | C、2i | D、-2i |
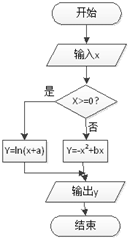 小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0.
小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0.