题目内容
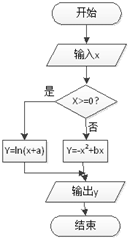 小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0.
小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0. (Ⅰ)求这个分段函数的解析式并计算f(f(-1));
(Ⅱ)若函数g(x)=f(x)-m有三个零点,求m的取值范围.
考点:程序框图,函数的零点
专题:算法和程序框图
分析:(Ⅰ)根据程序对应的条件,即可求这个分段函数的解析式,代入即可计算f(f(-1));
(Ⅱ)由g(x)=f(x)-m=0,得到f(x)=m,根据函数零点和方程根的关系即可求m的取值范围.
(Ⅱ)由g(x)=f(x)-m=0,得到f(x)=m,根据函数零点和方程根的关系即可求m的取值范围.
解答:
解:(1)根据程序框图可知:由lna=0得:a=1,
由-(-2)2-2b=0得:b=-2,
∴f(x)=
,
∴f(f(-1))=ln2.
(2)由g(x)=f(x)-m=0得:m=f(x),
在平面直角坐标系中作出y=f(x)的图象,
数形结合可得:0<m<1.
由-(-2)2-2b=0得:b=-2,
∴f(x)=
|
∴f(f(-1))=ln2.
(2)由g(x)=f(x)-m=0得:m=f(x),

在平面直角坐标系中作出y=f(x)的图象,
数形结合可得:0<m<1.
点评:本题主要考查程序框图的识别和应用,以及函数零点个数的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
已知A、B、C三点共线,O是这条直线外一点,设
=
,
=
,
=
,且存在实数m,使m
-3
-
=
成立,则点A分
的比为( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| 0 |
| BC |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
(理)已知数列{an}的通项公式an=n2-(6+2λ)n+2014,若a6或a7为数列{an}的最小项,则实数λ的取值范围( )
| A、(3,4) | ||||
| B、[2,5] | ||||
| C、[3,4] | ||||
D、[
|
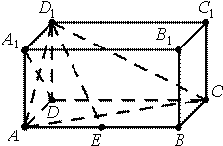 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.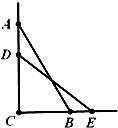 如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,
如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,