题目内容

数列{an}、{bn}的每一项都是正数，a1=8，b1=16，且an、bn、an+1成等差数列，bn、an+1、bn+1成等比数列，n=1，2，3，…．
（Ⅰ）求a2、b2的值；
（Ⅱ）求数列{an}、{bn}的通项公式；
（Ⅲ）证明：对一切正整数n，有
1
a1-1
+
1
a2-1
+
1
a3-1
+…+
1
an-1
＜
2
7
．
考点：数列与不等式的综合,数列的求和
专题：等差数列与等比数列
分析：（Ⅰ）由已知条件得2b1=a1+a2，
a
2
2
=b1b2，由此能求出a2、b2的值．
（Ⅱ）由已知条件推导出2bn=an+an+1．
a
2
n+1
=bnbn+1，an+1=
bnbn+1
，由此能求出bn=4(n+1)2，an=4n（n+1）．
（Ⅲ）由（Ⅱ）可知，所证明的不等式为
1
7
+
1
23
+
1
47
+…+
1
4n2+4n-1
＜
2
7
，可以用三种不同的方法进行证明．
解答： （本题满分14分）
（Ⅰ）解：∵a1=8，b1=16，且an、bn、an+1成等差数列，
∴2b1=a1+a2，得a2=2b1-a1=32-8=24．…（1分）
∵bn、an+1、bn+1成等比数列，
∴
a
2
2
=b1b2，得b2=
a
2
2
b1
=36．…（2分）
（Ⅱ）解：∵an、bn、an+1成等差数列，∴2bn=an+an+1…①．…（3分）
∵bn、an+1、bn+1成等比数列，∴
a
2
n+1
=bnbn+1，
∵数列{an}、{bn}的每一项都是正数，∴an+1=
bnbn+1
…②．…（4分）
∴当n≥2时，an=
bn-1bn
…③．…（5分）
将②、③代入①式，得2
bn
=
bn-1
+
bn+1
，
∴数列{
bn
}是首项为4，公差为2的等差数列，
∴
bn
=
b1
+(n-1)d=2n+2，
∴bn=4(n+1)2．…（6分）
由③式得当n≥2时，an=
bn-1bn
=
4n2•4(n+1)2
=4n(n+1)．…（7分）
当n=1时，a1=8，满足该式子，
∴对一切正整数n，都有an=4n（n+1）．…（8分）
（Ⅲ）证明：由（Ⅱ）可知，所证明的不等式为
1
7
+
1
23
+
1
47
+…+
1
4n2+4n-1
＜
2
7
．…（9分）
方法一：首先证明
1
4n2+4n-1
＜
2
7
(
1
n
-
1
n+1
)（n≥2）．
∵
1
4n2+4n-1
＜
2
7
(
1
n
-
1
n+1
)?
1
4n2+4n-1
＜
2
7n2+7n
?7n2+7n＜8n2+8n-2，
∴n2+n-2＞0?（n-1）（n+2）＞0，
所以当n≥2时，
1
7
+
1
23
+…+
1
4n2+4n-1
＜
1
7
+
2
7
[(
1
2
-
1
3
)+…+(
1
n
-
1
n+1
)]＜
1
7
+
2
7
×
1
2
=
2
7
．…（12分）
当n=1时，
1
7
＜
2
7
．…（13分）
综上所述，对一切正整数n，有
1
a1-1
+
1
a2-1
+
1
a3-1
+…+
1
an-1
＜
2
7
…（14分）
方法二：
1
4n2+4n-1
＜
1
4n2+4n-3
=
1
(2n-1)(2n+3)
=
1
4
(
1
2n-1
-
1
2n+3
)．
当n≥3时，
1
7
+
1
23
+…+
1
4n2+4n-1
＜
1
7
+
1
23
+
1
4
[(
1
5
-
1
9
)+(
1
7
-
1
11
)+…+(
1
2n-3
-
1
2n+1
)+(
1
2n-1
-
1
2n+3
)]＜
1
7
+
1
23
+
1
4
(
1
5
+
1
7
)＜
1
7
+
1
14
+
1
14
=
2
7
．…（12分）
当n=1时，
1
7
＜
2
7
；当n=2时，
1
7
+
1
23
＜
1
7
+
1
7
=
2
7
．…（13分）
综上所述，对一切正整数n，有
1
a1-1
+
1
a2-1
+
1
a3-1
+…+
1
an-1
＜
2
7
…（14分）
方法三：
1
4n2+4n-1
＜
1
4n2-1
=
1
(2n-1)(2n+1)
=
1
2
(
1
2n-1
-
1
2n+1
)．
当n≥4时，
1
7
+
1
23
+…+
1
4n2+4n-1
＜
1
7
+
1
23
+
1
47
+
1
2
[(
1
7
-
1
9
)+(
1
9
-
1
11
)+…+(
1
2n-3
-
1
2n-1
)+(
1
2n-1
-
1
2n+1
)]＜
1
7
+
1
23
+
1
47
+
1
14
＜
2
7
．…（12分）
当n=1时，
1
7
＜
2
7
；当n=2时，
1
7
+
1
23
＜
1
7
+
1
7
=
2
7
；
当n=3时，
1
7
+
1
23
+
1
47
＜
1
7
+
1
14
+
1
14
=
2
7
．…（13分）
综上所述，对一切正整数n，有
1
a1-1
+
1
a2-1
+
1
a3-1
+…+
1
an-1
＜
2
7
…（14分）．
点评：本题考查数列的通项公式的求法，考查不等式的证明，一题多证能够培养学生举一反三的能力．
练习册系列答案
相关题目
在三棱锥P-ABC中，PA垂直于底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=AB=2，∠BPC=θ，则当△AEF的面积最大时，tanθ的值为
 
．
已知A、B、C三点共线，O是这条直线外一点，设
OA
=
a
，
OB
=
b
，
OC
=
c
，且存在实数m，使m
a
-3
b
-
c
=
0
成立，则点A分
BC
的比为（　　）
A、-
1
3
B、-
1
2
C、
1
3
D、
1
2
已知数列{an}是等比数列，且a1+a3=-3，a2a4=4，则公比q的值是（　　）
A、
2
B、-2
C、±
2
D、±2
阜阳三中新校区计划在2013年招聘生活老师，要求男性x名，女性y名，x和y须满足约束条件
2x-y≥5
x-y≤2
x≤6
，则阜阳三中在2013年招聘的生活老师最多（　　）名．
A、9B、10C、13D、14
已知{an}是等差数列，首项a1=3，前n项和为Sn．令cn=(-1)nSn(n∈N*)，{cn}的前20项和T20=330．数列{bn}是公比为q的等比数列，前n项和为Wn，且b1=2，q3=a9．
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）证明：(3n+1)Wn≥nWn+1(n∈N*)．
设Sn表示数列{an}的前n项和．
（1）若{an}为公比为q的等比数列，写出并推导Sn的计算公式；
（2）若an=2n，bn=nlog2（Sn+2），求证：
1
b1
+
1
b2
+…+
1
bn
＜1．
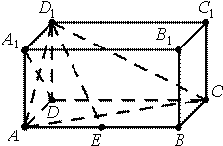如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．
（1）求异面直线D1E与A1D所成角．
（2）（文）当E为AB中点时，求点E到平面ACD1的距离．
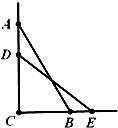如图，一根长为2米的木棒AB斜靠在墙壁AC上，∠ABC=60°，若AB滑动至DE位置，
且AD=(
3
-
2
) 米，问木棒AB中点O所经过的路程为
 
米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网