题目内容
已知数列{an}的通项公式为an=25-n,数列{bn}的通项公式为bn=n+k,设cn=
若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是 .
|
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:若c5=a5,则b6≥a5,a5>b5,b6≥a5,由此推导出-5≤k<-4;若c5=b5,则b5≥a5,b5≥a5,a4≥b5,由此推导出-5≤k≤-3.由此能求出实数k的取值范围.
解答:
解:若c5=a5,则a5>b5,则前面不会有bn的项,
∵{bn}递增,{an}递减,∴bi(i=1,2,3,4)<b5<a5<ai(i=1,2,3,4),
∵an递减,∴当n≥6时,必有cn≠an,即cn=bn,
此时应有b6≥a5,∴a5>b5,即20>5+k,得k<-4,
b6≥a5,即6+k≥1,得k≥-5,
∴-5≤k<-4.
若c5=b5,则b5≥a5,同理,前面不能有bn项,
即a4≥b5>b4,当n≥6时,∵{bn}递增,{an}递减,
∴bn>b5≥a5>an(n≥6),
∴当n≥6时,cn=bn.由b5≥a5,即5+k≥1,得,k≥-4,
由a4≥b5,得2≥5+k,得k≤-3,即-4≤k≤-3.
综上得,-5≤k≤-3.
∴实数k的取值范围是[-5,-3].
故答案为:[-5,-3].
∵{bn}递增,{an}递减,∴bi(i=1,2,3,4)<b5<a5<ai(i=1,2,3,4),
∵an递减,∴当n≥6时,必有cn≠an,即cn=bn,
此时应有b6≥a5,∴a5>b5,即20>5+k,得k<-4,
b6≥a5,即6+k≥1,得k≥-5,
∴-5≤k<-4.
若c5=b5,则b5≥a5,同理,前面不能有bn项,
即a4≥b5>b4,当n≥6时,∵{bn}递增,{an}递减,
∴bn>b5≥a5>an(n≥6),
∴当n≥6时,cn=bn.由b5≥a5,即5+k≥1,得,k≥-4,
由a4≥b5,得2≥5+k,得k≤-3,即-4≤k≤-3.
综上得,-5≤k≤-3.
∴实数k的取值范围是[-5,-3].
故答案为:[-5,-3].
点评:本题考查实数的取值范围的求法,综合性强,难度大,解题时要熟练掌握等差数列和等比数列的性质的灵活运用.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
某算法的程序框图如图所示,若输入a=1,b=2,c=3,则输出的结果为( )


| A、1 | B、2 | C、3 | D、4 |
若|
|=2|
|≠0,
⊥
,
=
+
,则
与
的夹角为( )
| b |
| a |
| c |
| a |
| c |
| a |
| b |
| a |
| b |
| A、30° | B、60° |
| C、90° | D、120° |
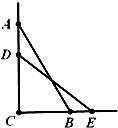 如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,
如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,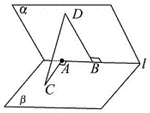 如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为
如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为