题目内容
设函数f(x)=x2+|x-1|+2a,a∈R.
(1)若方程f(x)=3x在(1,2)上有根,求a的取值范围;
(2)设g(x)=log2(-4x+a+1),若对任意的x1、x2∈(0,2),都有g(x1)<f(x2)+
,求a的取值范围.
(1)若方程f(x)=3x在(1,2)上有根,求a的取值范围;
(2)设g(x)=log2(-4x+a+1),若对任意的x1、x2∈(0,2),都有g(x1)<f(x2)+
| 21 |
| 4 |
考点:对数函数图象与性质的综合应用,二次函数的性质
专题:函数的性质及应用
分析:(1)由题意可得函数h(x)=f(x)-3x=x2+|x-1|-3x+2a 在(1,2)上有零点,h(1)h(2)=(2a-2)•(2a-1)<0,由此求得a的范围.
(2)由g(x)的单调性可得g(x)<g(0)=log2(-4a+1),求得f(x)的最小值为f(
)=2a+
,可得log2(-4a+1)≤2a+
+
=log222a+6,即 7•22a≥1,由此求得a的范围.
(2)由g(x)的单调性可得g(x)<g(0)=log2(-4a+1),求得f(x)的最小值为f(
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 21 |
| 4 |
解答:
解:(1)∵方程f(x)=3x在(1,2)上有根,∴函数h(x)=f(x)-3x=x2+|x-1|-3x+2a 在(1,2)上有零点.
由于在(1,2)上,h(x)=f(x)-3x=x2 -2x+2a-1是增函数,故有h(1)h(2)=(2a-2)•(2a-1)<0,
求得
<a<1.
(2)g(x)=log2(-4x+a+1)在(0,2)上是减函数,故g(x)<g(0)=log2(-4a+1).
而在(0,2)上,f(x)=
,∴f(x)的最小值为f(
)=2a+
,
由题意可得,log2(-4a+1)≤2a+
+
=2a+6=log222a+6,∴1-22a≤22a+6,即 7•22a≥1,
即 2a≥log2
,求得 a≥
log2
=-
log27,即a的范围为[-
log27,+∞).
由于在(1,2)上,h(x)=f(x)-3x=x2 -2x+2a-1是增函数,故有h(1)h(2)=(2a-2)•(2a-1)<0,
求得
| 1 |
| 2 |
(2)g(x)=log2(-4x+a+1)在(0,2)上是减函数,故g(x)<g(0)=log2(-4a+1).
而在(0,2)上,f(x)=
|
| 1 |
| 2 |
| 3 |
| 4 |
由题意可得,log2(-4a+1)≤2a+
| 3 |
| 4 |
| 21 |
| 4 |
即 2a≥log2
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查对数函数的图象和性质的综合应用,函数的恒成立问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x∈R,则“x<1”是“x≠2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
f(x)=
则f[f(
)]=( )
|
| 1 |
| 9 |
| A、-2 | ||
| B、-3 | ||
| C、9 | ||
D、
|
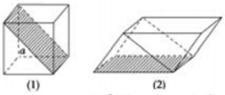 如图(1)所示,已知正方体面对角线长为a,沿阴影面将它切割成两块,拼成如图(2)所示的几何体,那么此几何体的表面积为( )
如图(1)所示,已知正方体面对角线长为a,沿阴影面将它切割成两块,拼成如图(2)所示的几何体,那么此几何体的表面积为( )A、(1+2
| ||
B、(2+
| ||
C、(3+2
| ||
D、(4+
|
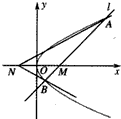 已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A、B两点,点N与点M关于y轴对称,
已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A、B两点,点N与点M关于y轴对称,