题目内容
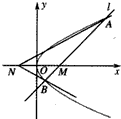 已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A、B两点,点N与点M关于y轴对称,
已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A、B两点,点N与点M关于y轴对称,(1)当a=1时,求证:∠ANM=∠BNM;
(2)对于给定的正数a,是否存在直线l′:x=m,使得l′被以AM为直径的圆所截得的弦长为定值?如果存在,求出直线l′的方程,如果不存在,试说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设l:x-1=ny,代入y2=4x得y2-4ny-4=0,根据韦达定理,表示出NB和NA斜率,求得斜率互为相反数,故∠ANM=∠BNM;
(2)假设满足条件的直线l存在,直线l'被圆O'截得的弦为EF,求出|EF|,分类讨论,即可得出结论.
(2)假设满足条件的直线l存在,直线l'被圆O'截得的弦为EF,求出|EF|,分类讨论,即可得出结论.
解答:
(1)证明:设l:x-1=ny,A(x1,y1),B(x2,y2)
代入y2=4x得y2-4ny-4=0,
∴y1+y2=4n,y1y2=-4
∴kAN+kBN=
+
=
=0,
∴∠ANM=∠BNM.
(2)解:设点A(x,y),则以AM为直径的圆的圆心为O(
,
),
假设满足条件的直线l存在,直线l'被圆O'截得的弦为EF,
则|EF|2=4[(
-a)2+
-(m-
)2]
=x2-2ax+a2+4x-4m2+4m(x+a)-x2-2ax-a2
=(4m-4a+4)x+4ma-4m2
弦长|EF|为定值,则4m-4a+4=0,即m=a-1,
此时|EF|2=4m(a-m)=4(a-1),
所以当a>1时,存在直线l:x=a-1,截得的弦长为2
当0<a≤1时,不存在满足条件的直线l'.
代入y2=4x得y2-4ny-4=0,
∴y1+y2=4n,y1y2=-4
∴kAN+kBN=
| y1 |
| x1+1 |
| y2 |
| x2+1 |
(
| ||
| (x1+1)(x2+1) |
∴∠ANM=∠BNM.
(2)解:设点A(x,y),则以AM为直径的圆的圆心为O(
| x+a |
| 2 |
| 1 |
| 2 |
假设满足条件的直线l存在,直线l'被圆O'截得的弦为EF,
则|EF|2=4[(
| x+a |
| 2 |
| y2 |
| 4 |
| x+a |
| 2 |
=x2-2ax+a2+4x-4m2+4m(x+a)-x2-2ax-a2
=(4m-4a+4)x+4ma-4m2
弦长|EF|为定值,则4m-4a+4=0,即m=a-1,
此时|EF|2=4m(a-m)=4(a-1),
所以当a>1时,存在直线l:x=a-1,截得的弦长为2
| a-1 |
当0<a≤1时,不存在满足条件的直线l'.
点评:本题考查弦长的计算和直线与抛物线位置关系的综合运用,解题时要注意分类讨论思想和弦长公式的合理运用,注意合理地进行等价转化.

练习册系列答案
相关题目
已知i是虚数单位,m.n∈R,则“m=n=1”是“(m-ni)2=-2i”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设集合M={0,1,2},N={x|x2=2x},则A∩B=( )
| A、{0,1,2} | B、{0,2} |
| C、{2} | D、{0} |
