题目内容

已知关于x的方程x2+（a+1）x+a+2b+1=0的两个实根分别为x1，x2，且0＜x1＜1，x2＞1，则
b
a
的取值范围是
 
．
考点：基本不等式
专题：不等式的解法及应用
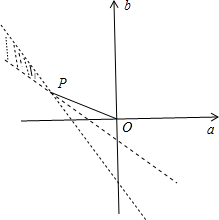
分析：令f（x）=x2+（a+1）x+a+2b+1，由于关于x的方程x2+（a+1）x+a+2b+1=0的两个实根分别为x1，x2，且0＜x1＜1，x2＞1，可得f（0）＞0，f（1）＜0，再利用线性规划的有关知识即可得出．
解答： 解：令f（x）=x2+（a+1）x+a+2b+1，
∵关于x的方程x2+（a+1）x+a+2b+1=0的两个实根分别为x1，x2，且0＜x1＜1，x2＞1，
∴f（0）＞0，f（1）＜0，
∴a+2b+1＞0，1+a+1+a+2b+1＜0，
即a+2b+1＞0，2a+2b+3＜0，
设
b
a
=k，即b=ka，
联立
a+2b+1=0
2a+2b+3=0
，解得P(-2，
1
2
)．
∴-1＜k＜-
1
4
，
故答案为：(-1，-
1
4
)．
点评：本题考查了二次函数的性质、线性规划的有关知识、一元二次方程有实数根的条件，属于中档题．
练习册系列答案
相关题目
下列五个命题：
①若一个圆锥的底面半径缩小到原来的
1
2
，其体积缩小到原来的
1
4
；
②若两组数据的中位数相等，则它们的平均数也相等；
③直线x+y+1=0与圆x2+y2=
1
2
相切；
④“10a≥10b”是“lga≥lgb”的充分不必要条件．
其中真命题的序号是：
 
．
已知函数f（x）=sinx+acosx的图象经过点（
π
3
，0）
（1）求实数a的值；
（2）设g（x）=[f（x）]2-2，求当x∈（
π
4
，
2π
3
）时，函数g（x）的值域；
（3）若g（
a
2
）=-
3
4
（
π
6
＜a＜
2π
3
），求cos（α+
3π
2
）的值．
函数f（x）=2sin（2x-
π
3
）+3的最小值为（　　）
A、5B、1C、3D、4
已知向量
a
=（1，2），
b
=（2，-2）．
（Ⅰ）求 
a
•
b
的值；
（Ⅱ）若 
a
+λ
b
与 
a
垂直，求λ的值．
已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的图象经过点（0，
1
2
），且相邻两条对称轴间的距离为
π
2
．
（Ⅰ）求函数f（x）的解析式及其单调递增区间；
（Ⅱ）在△ABC中，a，b，c分别是角A、B、C的对边，若f（
A
2
）-cosA=
1
2
，且bc=1，b+c=3，求a的值．
下面是关于公差d＞0的等差数列{an}的两个命题：p1：数列{nan}是递增数列；p2：数列{
an
n
}是递增数列．
其中的真命题为（　　）
A、p1∨p2
B、p1∧p2
C、￢p1∨p2
D、p1∧￢p2
函数f（x）=
1
2
sin2x-
3
2
cos2x+1的单调递增区间为
 
．
已知x，y均为正数，且
1
x
+
9
y
=1，求x+y的最小值及取得最小值时x，y的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网