题目内容
函数f（x）=2sin（2x-
）+3的最小值为（ ）
| π |
| 3 |
| A、5 | B、1 | C、3 | D、4 |
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：直接根据正弦型函数的最值求解析式的最小值．
解答：
解：f（x）=2sin（2x-
）+3
则：当2x-
=2kπ-
时，
即：x=kπ-
（k∈Z）
函数f（x）min=-2+3=1
故选：B
| π |
| 3 |
则：当2x-
| π |
| 3 |
| π |
| 2 |
即：x=kπ-
| π |
| 12 |
函数f（x）min=-2+3=1
故选：B
点评：本题考查的知识要点：正弦型三角函数的最值问题．属于基础题型．
练习册系列答案
相关题目
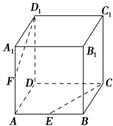如图，在正方体ABCD-A1B1C1D1中，E、F分别是AB和AA1的中点，则下列命题：