题目内容
已知向量
=（1，2），
=（2，-2）．
（Ⅰ）求
•
的值；
（Ⅱ）若
+λ
与
垂直，求λ的值．
| a |
| b |
（Ⅰ）求
| a |
| b |
（Ⅱ）若
| a |
| b |
| a |
考点：平面向量数量积的运算,数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：（Ⅰ）利用向量的坐标表示，直接求
•
的值；
（Ⅱ）求出
+λ
，利用两个向量垂直，数量积为0，即可求λ的值．
| a |
| b |
（Ⅱ）求出
| a |
| b |
解答：
解：（Ⅰ）
•
=1×2+2×(-2)=-2…（2分）
（Ⅱ） 由已知得
+λ
=(1+2λ， 2-2λ)…（4分）
由于
+λ
与
垂直，
∴1+2λ+2（2-2λ）=0…（6分）
∴λ=
…（7分）
| a |
| b |
（Ⅱ） 由已知得
| a |
| b |
由于
| a |
| b |
| a |
∴1+2λ+2（2-2λ）=0…（6分）
∴λ=
| 5 |
| 2 |
点评：本题考查向量的数量积的应用，向量的垂直，考查计算能力．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
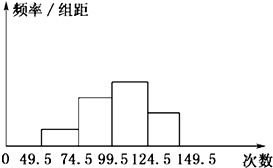为了了解小学生的体能情况，抽取了某校一个年级的部分学生进行一分钟跳绳次数测试，将取得的数据整理后，画出频率分布直方图（如图）．已知图中从左到右前三个小组的频率分别为0.1，0.3，0.4，且第一小组的频数为5．执行如图所示的程序框图，如果输出的结果为
，则判断框内可填入的条件是（ ）
| 31 |
| 16 |
| A、k＜4 | B、k＞4 |
| C、k＜5 | D、k＞5 |
命题“若x＞2，则x＞1”的逆命题是（ ）
| A、若x＞1，则x＞2 |
| B、若x≤2，则x≤1 |
| C、若x≤1，则x≤2 |
| D、若x＜2，则x＜1 |