题目内容
已知函数f(x)=sinx+acosx的图象经过点(
,0)
(1)求实数a的值;
(2)设g(x)=[f(x)]2-2,求当x∈(
,
)时,函数g(x)的值域;
(3)若g(
)=-
(
<a<
),求cos(α+
)的值.
| π |
| 3 |
(1)求实数a的值;
(2)设g(x)=[f(x)]2-2,求当x∈(
| π |
| 4 |
| 2π |
| 3 |
(3)若g(
| a |
| 2 |
| ||
| 4 |
| π |
| 6 |
| 2π |
| 3 |
| 3π |
| 2 |
考点:两角和与差的正弦函数,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)把点(
,0)代入解析式,求出a的值;
(2)先利用两角差的正弦公式化简f(x),代入g(x)利用二倍角公式化简,由x的范围求出2x-
的范围,利用余弦函数的性质求出g(x)的值域;
(3)代入解析式化简g(
)=-
,由α的范围和平方关系求出sin(α-
)的值,利用两角和的正弦公式求出sinα的值,利用诱导公式化简cos(α+
)后即可求值.
| π |
| 3 |
(2)先利用两角差的正弦公式化简f(x),代入g(x)利用二倍角公式化简,由x的范围求出2x-
| 2π |
| 3 |
(3)代入解析式化简g(
| a |
| 2 |
| ||
| 4 |
| 2π |
| 3 |
| 3π |
| 2 |
解答:
解:(1)因为函数f(x)=sinx+acosx的图象经过点(
,0),
所以sin
+acos
=0,解得a=-
;
(2)由(1)可得,f(x)=sinx-
cosx=2sin(x-
),
所以g(x)=[f(x)]2-2=4sin2(x-
)-2
=4×
-2=-2cos(2x-
),
由x∈(
,
)得,2x-
∈(-
,
),
则-
<cos(2x-
)≤1,所以-2≤-2cos(2x-
)<1,
则函数g(x)的值域:[-2,1);
(3)因为g(
)=-
,所以-2cos(α-
)=-
,即cos(α-
)=
,
因为
<a<
,所以-
<α-
<0,
则sin(α-
)=-
=-
,
所以sinα=sin[(α-
)+
]=sin(α-
)cos
+cos(α-
)sin
=-
×(-
)+
×
=
,
则cos(α+
)=sinα=
.
| π |
| 3 |
所以sin
| π |
| 3 |
| π |
| 3 |
| 3 |
(2)由(1)可得,f(x)=sinx-
| 3 |
| π |
| 3 |
所以g(x)=[f(x)]2-2=4sin2(x-
| π |
| 3 |
=4×
1-cos(2x-
| ||
| 2 |
| 2π |
| 3 |
由x∈(
| π |
| 4 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
则-
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
则函数g(x)的值域:[-2,1);
(3)因为g(
| a |
| 2 |
| ||
| 4 |
| 2π |
| 3 |
| ||
| 4 |
| 2π |
| 3 |
| ||
| 8 |
因为
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
则sin(α-
| 2π |
| 3 |
1-cos2(α-
|
| ||
| 8 |
所以sinα=sin[(α-
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=-
| ||
| 8 |
| 1 |
| 2 |
| ||
| 8 |
| ||
| 2 |
3+
| ||
| 16 |
则cos(α+
| 3π |
| 2 |
3+
| ||
| 16 |
点评:本题考查三角恒等变换的公式,平方关系、三角函数值的符号的应用,以及余弦函数的性质,注意角之间的关系和角的范围,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
双曲线
-
=1上一点P到它的一个焦点的距离等于1,那么点P到另一个焦点的距离为( )
| y2 |
| 16 |
| x2 |
| 4 |
| A、5 | B、7 | C、9 | D、17 |
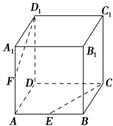 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点,则下列命题:
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点,则下列命题: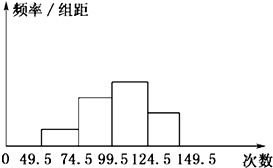 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.