题目内容
已知x，y均为正数，且
+
=1，求x+y的最小值及取得最小值时x，y的值．
| 1 |
| x |
| 9 |
| y |
考点：基本不等式
专题：不等式的解法及应用
分析：利用“乘1法”与基本不等式的性质即可得出．
解答：
解：∵x，y均为正数，且
+
=1，
∴x+y=(x+y)(
+
)=10+
+
≥10+2
=16，
当且仅当x=4时，等号成立，即（x+y）min=16．
| 1 |
| x |
| 9 |
| y |
∴x+y=(x+y)(
| 1 |
| x |
| 9 |
| y |
| y |
| x |
| 9x |
| y |
|
当且仅当x=4时，等号成立，即（x+y）min=16．
点评：本题考查了“乘1法”与基本不等式的性质，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
命题“若x＞2，则x＞1”的逆命题是（ ）
| A、若x＞1，则x＞2 |
| B、若x≤2，则x≤1 |
| C、若x≤1，则x≤2 |
| D、若x＜2，则x＜1 |
设集合A={x|x+2＞0}，B={x|y=
}，则A∩B=（ ）
| 1 | ||
|
| A、{x|x＞-2} |
| B、{x|x＜3} |
| C、{x|x＞3或x＜-2} |
| D、{x|-2＜x＜3} |
已知集合A={1，3，5，6}，集合B={2，3，4，5}，那么A∩B=（ ）
| A、{3，5} |
| B、{1，2，3，4，5，6} |
| C、{7} |
| D、{1，4，7} |
已知i是虚数单位，复数z1=1+2i，z2=3+4i，那么z1+z2=（ ）
| A、5+5i | B、4+6i |
| C、10i | D、10 |
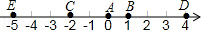如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样移动解答：