题目内容
12．某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）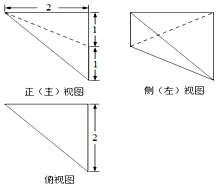
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | $\frac{4}{3}$ |
分析 由已知中的三视图可得：该几何体是一个以侧视图中右下角的三角形为底面的三棱锥，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得：该几何体是一个以侧视图中右下角的三角形为底面的三棱锥，
其底面面积S=$\frac{1}{2}$×2×2=2，高h=2，
故棱锥的体积V=$\frac{1}{3}×2×2$=$\frac{4}{3}$，
故选：D．
点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
2．函数$f（x）=ax-\frac{1}{2}{x^2}-4lnx$在区间[1，+∞）上为减函数，则实数a的取值范围是（ ）
| A． | （-∞，4） | B． | （-∞，4] | C． | （-∞，5） | D． | （-∞，5] |
3．某几何体的三视图如图所示，则其体积为（ ）
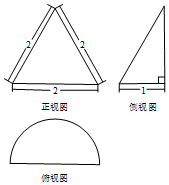
| A． | $\frac{{\sqrt{3}π}}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{{\sqrt{3}π}}{6}$ | D． | $\frac{{\sqrt{3}π}}{3}$ |
20．已知0＜a1＜a2＜a3，则使得${（{1-{a_i}x}）^2}＜1（{i=1，2，3}）$都成立的x的取值范围是（ ）
| A． | $（{0，\frac{1}{a_3}}）$ | B． | $（{0，\frac{2}{a_3}}）$ | C． | $（{0，\frac{1}{a_1}}）$ | D． | $（{0，\frac{2}{a_1}}）$ |
7．为了调查每天人们使用手机的时间，我校某课外兴趣小组在天府广场随机采访男性、女性用户各50 名，其中每天玩手机超过6小时的用户列为“手机控”，否则称其为“非手机控”，调查结果如下：
（1）根据以上数据，能否有60%的把握认为“手机控”与“性别”有关？
（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取5人中“手机控”和“非手机控”的人数；
（3）从（2）中抽取的5人中再随机抽取3人，记这3人中“手机控”的人数为X，试求X的分布列与数学期望．
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}，其中n=a+b+c+d$．
参考数据：
| 手机控 | 非手机控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取5人中“手机控”和“非手机控”的人数；
（3）从（2）中抽取的5人中再随机抽取3人，记这3人中“手机控”的人数为X，试求X的分布列与数学期望．
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}，其中n=a+b+c+d$．
参考数据：
| P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.456[ | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
17．某几何体的三视图如图所示，则该几何体的体积为（ ）
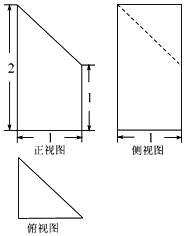
| A． | ${\frac{5}{6}_{\;}}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
2．已知全集U=R，集合M={x||x|＜1}，N={y|y=2x，x∈R}，则集合∁U（M∪N）等于（ ）
| A． | （-∞，-1] | B． | （-1，2） | C． | （-∞，-1]∪[2，+∞） | D． | [2，+∞） |