题目内容
7.为了调查每天人们使用手机的时间,我校某课外兴趣小组在天府广场随机采访男性、女性用户各50 名,其中每天玩手机超过6小时的用户列为“手机控”,否则称其为“非手机控”,调查结果如下:| 手机控 | 非手机控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取5人中“手机控”和“非手机控”的人数;
(3)从(2)中抽取的5人中再随机抽取3人,记这3人中“手机控”的人数为X,试求X的分布列与数学期望.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}},其中n=a+b+c+d$.
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.456[ | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
分析 (1)计算K2的值,与临界值比较,可得结论;
(2)从参与调查的女性用户中按分层抽样的方法,比例为3:2,可得结论.
(3)X的取值为1,2,3,再求出X取每一个值的概率,即可求得X的分布列和数学期望.
解答 解:$({1})由题意,{K^2}=\frac{{100×{{({26×20-30×24})}^2}}}{56×44×50×50}≈0.65<0.708$
∴没有60%的把握认为“手机控”与“性别”有关;
(2)从参与调查的女性用户中按分层抽样的方法,比例为3:2,所抽取的5人中“手机”有3人,“非手机控”的人数有2人;
(3)X=1,2,3,则$P(X=1)=\frac{C_3^1}{C_5^3}=0.3$$P(X=2)=\frac{C_3^2C_2^1}{C_5^3}=0.6$$P(X=3)=\frac{C_3^3}{C_5^3}=0.1$.
X的分布列为:
| X | 1 | 2 | 3 |
| P | 0.3 | 0.6 | 0.1 |
点评 本题主要考查独立性检验、分层抽样、离散型随机变量的分布列与数学期望,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
17.已知z∈C,“$z+\overline z=0$”是“z为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知集合$M=\left\{{x\left|{\frac{x-5}{x+1}≤0}\right.}\right\}$,N={-3,-1,1,3,5},则M∩N=( )
| A. | {-3,-1,1,3,5} | B. | {-1,1,3,5} | C. | {1,3,5} | D. | {-3,-1,1,3,} |
2.如图所示,图中粗线画出的是某几何体的三视图,该几何体的体积是( )
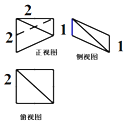

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
12.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
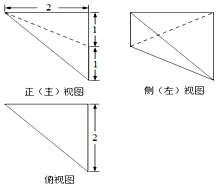

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |