题目内容
1.平面向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=4,|\overrightarrow b|=2$,$\overrightarrow a+\overrightarrow b$在$\overrightarrow a$上的投影为5,则$|\overrightarrow a-2\overrightarrow b|$的模为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 根据$\overrightarrow{a}+\overrightarrow{b}$在$\overrightarrow{a}$上的投影为5即可得出$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}|}=5$,从而可求出$\overrightarrow{a}•\overrightarrow{b}$的值,进而可求出$(\overrightarrow{a}-2\overrightarrow{b})^{2}$的值,从而便可得出$|\overrightarrow{a}-2\overrightarrow{b}|$的值.
解答 解:根据条件,
$|\overrightarrow{a}+\overrightarrow{b}|cos<(\overrightarrow{a}+\overrightarrow{b}),\overrightarrow{a}>$
=$|\overrightarrow{a}+\overrightarrow{b}|•\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+\overrightarrow{b}||\overrightarrow{a}|}$
=$\frac{{\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$
=$\frac{16+\overrightarrow{a}•\overrightarrow{b}}{4}$
=5;
∴$\overrightarrow{a}•\overrightarrow{b}=4$;
∴$(\overrightarrow{a}-2\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}=16-16+16=16$;
∴$|\overrightarrow{a}-2\overrightarrow{b}|=4$.
故选B.
点评 考查投影的概念及计算公式,向量夹角的余弦公式,以及向量数量积的运算及计算公式.

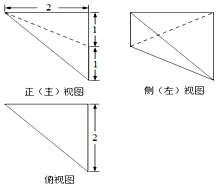
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
| A. | $\frac{7}{5}$ | B. | $\frac{6}{5}$ | C. | 4 | D. | 5 |
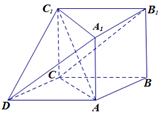 如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.
如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.