题目内容
17.某几何体的三视图如图所示,则该几何体的体积为( )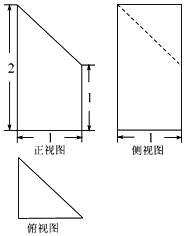
| A. | ${\frac{5}{6}_{\;}}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 根据已知中的三视图,可得该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥得到的组合体,可得答案.
解答 解:根据已知中的三视图,可得该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥得到的组合体,
其底面面积S=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
柱体的高为:2,锥体的高为1,
故组合体的体积V=$\frac{1}{2}$×2-$\frac{1}{3}$×$\frac{1}{2}$×1=${\frac{5}{6}_{\;}}$,
故选:A.
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
7.极坐标方程3ρsin2θ+cosθ=0表示的曲线是( )
| A. | 抛物线 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
8.已知-2,a1,a2,-8成等差数列,-2,b1,b2,b3,-8成等比数列,则$\frac{{a}_{2}-{a}_{1}}{{b}_{2}}$等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$或-$\frac{1}{2}$ |
12.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
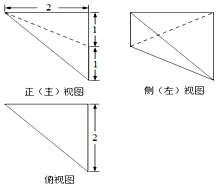

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
2.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,若对任意给定的y∈(2,+∞),都存在唯一的x∈R,满足f(f(x))=2a2y2+ay,则正实数a的最小值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
9.函数y=loga(x-3)+2(a>0,a≠1)的图象过定点P,且角α的终边过点P,则的值为sin2α+cos2α( )
| A. | $\frac{7}{5}$ | B. | $\frac{6}{5}$ | C. | 4 | D. | 5 |
6.设函数f(x)是R上的奇函数,f(x+π)=-f(x),当0≤x≤$\frac{π}{2}$时,f(x)=cosx-1,则-2π≤x≤2π时,f(x)的图象与x轴所围成图形的面积为( )
| A. | 4π-8 | B. | 2π-4 | C. | π-2 | D. | 3π-6 |
7.已知函数f(x)=aln(x+1)-x2,若对?p,q∈(0,1),且p≠q,有$\frac{{f({p+1})-f({q+1})}}{p-q}>2$恒成立,则实数a的取值范围为( )
| A. | (-∞,18) | B. | (-∞,18] | C. | [18,+∞) | D. | (18,+∞) |