题目内容
4.在二项式${({\root{3}{x}-\frac{2}{x}})^n}$的展开式中,所有项的二项式系数之和为256,则常数项为112.分析 由题意可得:2n=256,解得n,利用通项公式即可得出.
解答 解:由题意可得:2n=256,解得n=8.
$(\root{3}{x}-\frac{2}{x})^{8}$的通项公式为:Tr+1=${∁}_{8}^{r}$$(\root{3}{x})^{8-r}$$(-\frac{2}{x})^{r}$=(-2)r${∁}_{8}^{r}$${x}^{\frac{8-4r}{3}}$.
令$\frac{8-4r}{3}$=0,解得r=2.
∴常数项=$(-2)^{2}{∁}_{8}^{2}$=112.
故答案为:112.
点评 本题考查了二项式定理的通项公式及其性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数f(x)=ln|1-x|的图象大致形状是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知集合$M=\left\{{x\left|{\frac{x-5}{x+1}≤0}\right.}\right\}$,N={-3,-1,1,3,5},则M∩N=( )
| A. | {-3,-1,1,3,5} | B. | {-1,1,3,5} | C. | {1,3,5} | D. | {-3,-1,1,3,} |
12.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
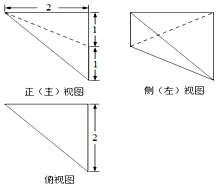

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
9.函数y=loga(x-3)+2(a>0,a≠1)的图象过定点P,且角α的终边过点P,则的值为sin2α+cos2α( )
| A. | $\frac{7}{5}$ | B. | $\frac{6}{5}$ | C. | 4 | D. | 5 |





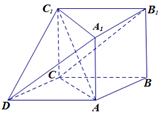 如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.
如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.