题目内容
2.函数$f(x)=ax-\frac{1}{2}{x^2}-4lnx$在区间[1,+∞)上为减函数,则实数a的取值范围是( )| A. | (-∞,4) | B. | (-∞,4] | C. | (-∞,5) | D. | (-∞,5] |
分析 要使函数f(x)在区间(1,+∞)上是减函数,我们可以转化为f′(x)≤0在区间(1,+∞)上恒成立的问题来求解,然后利用二次函数的单调区间于对称轴的关系来解答也可达到目标.
解答 解:∵函数$f(x)=ax-\frac{1}{2}{x^2}-4lnx$,在区间[1,+∞)上为减函数,
∴f′(x)=-$\frac{4}{x}$-x+a=$\frac{-{x}^{2}+ax-4}{x}$,
由f(x)在区间(1,+∞)上是减函数,可得-x2+ax-4≤0在区间[1,+∞)上恒成立
可得△≤0或$\left\{\begin{array}{l}{\frac{a}{2}≤1}\\{a-5≤0}\end{array}\right.$,即a2-16≤0或a≤2.
解得-4≤a≤4或a≤2,
故a的取值范围为:(-∞,4].
故选:B.
点评 本题以函数为载体,综合考查利用函数的导数来解决有关函数的单调性,考查已知函数的单调性的条件下怎样求解参数的范围问题,考查分类讨论,函数与方程,等数学思想与方法.

练习册系列答案
相关题目
10.已知xy>0,则$\frac{y}{x+y}+\frac{2x}{2x+y}$的最小值为( )
| A. | $4+2\sqrt{2}$ | B. | $4-2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 1 |
17.已知z∈C,“$z+\overline z=0$”是“z为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.极坐标方程3ρsin2θ+cosθ=0表示的曲线是( )
| A. | 抛物线 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
14.函数f(x)=ln|1-x|的图象大致形状是( )
| A. |  | B. |  | C. |  | D. |  |
12.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
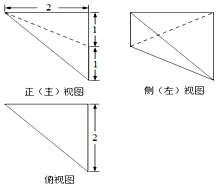

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
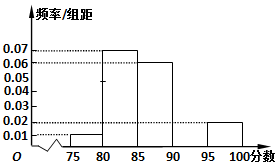 某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.