题目内容
 如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=
如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=| 1 |
| 2 |
考点:平行线分线段成比例定理
专题:立体几何
分析:连接BE,交FM的延长线于T,构造两个三角形△BEG和△BEA,运用中位线定理证明.
解答:
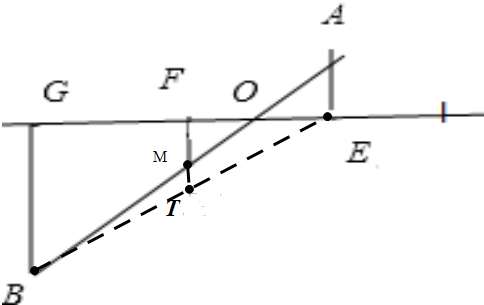 证明;连接BE,交FM的延长线于T,
证明;连接BE,交FM的延长线于T,
∵如图,直线l与AB交于点O,点M是AB的中点,
过点A、M、B分别作l的垂线,垂足分别是E、F、G.
∴T是BE的中点,FT∥BG,MT∥AE,
在△BEG中,FT是中位线,即FT=
BG,
在△BEA中,MT是中位线,即MT=
AE,
FM=FT-MT=
BG-
AE=
(BG-AE).
即FM=
(BG-AE)成立.
 证明;连接BE,交FM的延长线于T,
证明;连接BE,交FM的延长线于T,∵如图,直线l与AB交于点O,点M是AB的中点,
过点A、M、B分别作l的垂线,垂足分别是E、F、G.
∴T是BE的中点,FT∥BG,MT∥AE,
在△BEG中,FT是中位线,即FT=
| 1 |
| 2 |
在△BEA中,MT是中位线,即MT=
| 1 |
| 2 |
FM=FT-MT=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即FM=
| 1 |
| 2 |
点评:本题考查了运用构造三角形的方法,利用三角形的中位线定理证明线段的等量关系问题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
下面是关于公差d>0的等差数列(an)的四个命题:p1:数列{an}是递增数列;p2:数列{nan}是递增数列;p3:数列{
}是递增数列;p4:数列{an+3nd}是递增数列;其中的真命题为 .
| an |
| n |
下列叙述正确的是( )
| A、若|a|=a,则a>0 |
| B、若a≠b,则|a|≠|b| |
| C、若|a|=|b|,则a=b |
| D、若a=-b,则|a|=|b| |