题目内容
函数f(x)=
,其中x∈[2,5]
(1)判断函数的单调性并证明;
(2)若a<b,且a∈[2,5],b∈[2,5],比较f(a)和f(b)大小,并说明理由.
| 2 |
| x-1 |
(1)判断函数的单调性并证明;
(2)若a<b,且a∈[2,5],b∈[2,5],比较f(a)和f(b)大小,并说明理由.
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用,导数的综合应用
分析:(1)求f′(x),根据f′(x)的符号即可判断函数f(x)的单调性;
(2)因为a,b∈[2,5],且a<b,所以根据f(x)在[2,5]上的单调性即可判断f(a),f(b)的大小.
(2)因为a,b∈[2,5],且a<b,所以根据f(x)在[2,5]上的单调性即可判断f(a),f(b)的大小.
解答:
解:(1)f′(x)=-
<0;
∴函数f(x)在[2,5]上是减函数;
(2)∵f(x)在[2,5]上是减函数,a,b∈[2,5],且a<b,所以f(a)>f(b).
| 2 |
| (x-1)2 |
∴函数f(x)在[2,5]上是减函数;
(2)∵f(x)在[2,5]上是减函数,a,b∈[2,5],且a<b,所以f(a)>f(b).
点评:考查通过判断函数导数的符号判断函数单调性的方法,以及根据函数单调性比较函数值的大小.

练习册系列答案
相关题目
已知函数f(x)=
,则f(-7)=( )
|
| A、1 | B、4 | C、16 | D、49 |
给出下列函数①f(x)=(
)x;②f(x)=x2;③f(x)=sinx,x∈(-
,0);④f(x)=x
;⑤f(x)=log2x.其中满足条件f (
)>
(0<x1<x2)的函数的个数是( )
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
将函数y=
cosx+sinx(x∈R)的图象向左平移m(m>0)个长度单位后,所得到的图象关于原点对称,则m的最小值是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)是R上的可导函数,f(x)的导数f′(x)的图象如图,则下列结论正确的是( )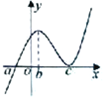

| A、a,c分别是极大值点和极小值点 |
| B、b,c分别是极大值点和极小值点 |
| C、f(x)在区间(a,c)上是增函数 |
| D、f(x)在区间(b,c)上是减函数 |
 如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=
如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=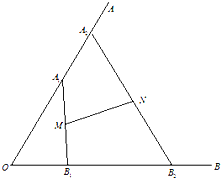 如图,∠AOB=
如图,∠AOB=