题目内容
已知动圆P与圆C1:(x+1)2+y2=
外切,与圆C2(x-1)2+y2=
内切.
(1)求动圆的圆心P的轨迹C的方程;
(2)设点M(
,0),是否存在过点F(1,0)且与x轴不垂直的直线l与轨迹C交于A、B两点,使得
+
⊥
?若存在,求出直线l的方程;若不存在,说明理由.
| 1 |
| 8 |
| 49 |
| 8 |
(1)求动圆的圆心P的轨迹C的方程;
(2)设点M(
| 1 |
| 4 |
| MA |
| MB |
| AB |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:向量与圆锥曲线
分析:(1)由两圆的位置关系得到|PC1|+|PC2|=2
>|C1C2|=2,由此可知动点P的轨迹为以C1,C2为焦点的椭圆,并求得长半轴长及半焦距,利用隐含条件求得b,则椭圆方程可求;
(2)假设存在这样的直线l,并设其方程为y=k(x-1),由点差法结合(
+
)⊥
得到k的值,则直线l的方程可求.
| 2 |
(2)假设存在这样的直线l,并设其方程为y=k(x-1),由点差法结合(
| MA |
| MB |
| AB |
解答:
解:(1)设动圆P的半径为r,由条件有:
,
则|PC1|+|PC2|=2
>|C1C2|=2,
∴动点P的轨迹为以C1,C2为焦点的椭圆,且2a=2
,c=1,
∴b2=a2-c2=1.
则所求轨迹的方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),A,B的中点为N(x0,y0),
假设存在这样的直线l,并设其方程为y=k(x-1),
由
,得(1+2k2)x2-4k2x+2k2-2=0.
又
,则
+(y1-y2)(y1+y2)=0.
即x0+2ky0=0,①
由(
+
)⊥
,得k•
=-1,②
联立①②得:x0=
,又x0=
=
,
∴k=±
.
∴这样的直线l存在,其方程为y=±
(x-1).
|
则|PC1|+|PC2|=2
| 2 |
∴动点P的轨迹为以C1,C2为焦点的椭圆,且2a=2
| 2 |
∴b2=a2-c2=1.
则所求轨迹的方程为
| x2 |
| 2 |
(2)设A(x1,y1),B(x2,y2),A,B的中点为N(x0,y0),
假设存在这样的直线l,并设其方程为y=k(x-1),
由
|
又
|
| (x1-x2)(x1+x2) |
| 2 |
即x0+2ky0=0,①
由(
| MA |
| MB |
| AB |
| y0 | ||
x0-
|
联立①②得:x0=
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 2k2 |
| 1+k2 |
∴k=±
| ||
| 2 |
∴这样的直线l存在,其方程为y=±
| ||
| 2 |
点评:本题考查了椭圆的定义,考查了直线与圆锥曲线的关系,训练了点差法求与中点弦有关的问题,是压轴题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
设a,b为实数,则“a>b>0是
<
”的( )
| 1 |
| a |
| 1 |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
不等式组
表示的平面区域的面积是( )
|
| A、30 | B、30.2 |
| C、30.25 | D、30.35 |
 已知四边形ABCD是边长为1的正方形,MA⊥平面ABCD,MA=2动点P在正方形的边上从点A出发经过点B运动到点C.设点P走过的路程为x,△MAP的面积为S(x),则函数y=S2(x)的图象是( )
已知四边形ABCD是边长为1的正方形,MA⊥平面ABCD,MA=2动点P在正方形的边上从点A出发经过点B运动到点C.设点P走过的路程为x,△MAP的面积为S(x),则函数y=S2(x)的图象是( )A、 |
B、 |
C、 |
D、 |
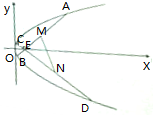 已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点.
已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点. 如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=
如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=