题目内容
已知圆O:x2+y2=1.
(1)已知直线l:ax+by+c=0,且满足条件3(a2+b2)=4c2,试判断直线与圆O的位置关系;
(2)求
的取值范围;
(3)圆O上有两点到直线y=kx+2的距离为
,求k的取值范围.
(1)已知直线l:ax+by+c=0,且满足条件3(a2+b2)=4c2,试判断直线与圆O的位置关系;
(2)求
| y-1 |
| x-2 |
(3)圆O上有两点到直线y=kx+2的距离为
| 1 |
| 2 |
考点:直线与圆的位置关系,点到直线的距离公式
专题:综合题,直线与圆
分析:(1)判断圆心到直线的距离为
=
<1,可得直线与圆O的位置关系;
(2)设
=k,圆心到直线的距离d=
≤1,求
的取值范围;
(3)圆O上有两点到直线y=kx+2的距离为
,圆心到直线的距离小于等于
,求k的取值范围.
| |c| | ||
|
| ||
| 2 |
(2)设
| y-1 |
| x-2 |
| |-2k+1| | ||
|
| y-1 |
| x-2 |
(3)圆O上有两点到直线y=kx+2的距离为
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵3(a2+b2)=4c2,
∴圆心到直线的距离为
=
<1,
∴直线与圆O相交;
(2)
=k,则y-1=k(x-2),即kx-y-2k+1=0,
圆心到直线的距离d=
≤1,
∴-
≤k≤0;
(3)∵圆O上有两点到直线y=kx+2的距离为
,
∴圆心到直线的距离小于等于
,
∴
≤
,
∴k≤-
或k≥
.
∴圆心到直线的距离为
| |c| | ||
|
| ||
| 2 |
∴直线与圆O相交;
(2)
| y-1 |
| x-2 |
圆心到直线的距离d=
| |-2k+1| | ||
|
∴-
| 4 |
| 3 |
(3)∵圆O上有两点到直线y=kx+2的距离为
| 1 |
| 2 |
∴圆心到直线的距离小于等于
| 1 |
| 2 |
∴
| 2 | ||
|
| 1 |
| 2 |
∴k≤-
| 15 |
| 15 |
点评:本题考查直线与圆的位置关系,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
设等差数列{an}满足:a1+a4+a7=12,则a1+a2+a3+…+a7=( )
| A、14 | B、21 | C、28 | D、35 |
给出下列函数①f(x)=(
)x;②f(x)=x2;③f(x)=sinx,x∈(-
,0);④f(x)=x
;⑤f(x)=log2x.其中满足条件f (
)>
(0<x1<x2)的函数的个数是( )
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
将函数y=
cosx+sinx(x∈R)的图象向左平移m(m>0)个长度单位后,所得到的图象关于原点对称,则m的最小值是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
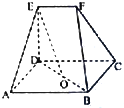 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=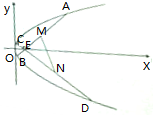 已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点.
已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点. 如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=
如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM= 已知四边形ABCD是边长为1的正方形,MA⊥平面ABCD,MA=2动点P在正方形的边上从点A出发经过点B运动到点C.设点P走过的路程为x,△MAP的面积为S(x),则函数y=S2(x)的图象是( )
已知四边形ABCD是边长为1的正方形,MA⊥平面ABCD,MA=2动点P在正方形的边上从点A出发经过点B运动到点C.设点P走过的路程为x,△MAP的面积为S(x),则函数y=S2(x)的图象是( )


