题目内容
下面是关于公差d>0的等差数列(an)的四个命题:p1:数列{an}是递增数列;p2:数列{nan}是递增数列;p3:数列{
}是递增数列;p4:数列{an+3nd}是递增数列;其中的真命题为 .
| an |
| n |
考点:命题的真假判断与应用
专题:推理和证明
分析:对于p1,与p4的正确性要证明,对于p2与p3举个反例即可.
解答:
解:∵d>0,∴d=an+1-an>0,∴an+1>an,∴数列{an}是递增数列,p1是真命题.
p2是假命题,如an=n-9是公差d=1>0的等差数列,但{nan}不是递增数列.同理可证
p3也是假命题.
对于p4是真命题,∵[an+1+3(n+1)d]-[an+3nd]=4d,∴数列{an+3nd}是递增数列.
故答案应为:p1,p4
p2是假命题,如an=n-9是公差d=1>0的等差数列,但{nan}不是递增数列.同理可证
p3也是假命题.
对于p4是真命题,∵[an+1+3(n+1)d]-[an+3nd]=4d,∴数列{an+3nd}是递增数列.
故答案应为:p1,p4
点评:本题借助数列考查命题的判断,属于基础题

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
设等差数列{an}满足:a1+a4+a7=12,则a1+a2+a3+…+a7=( )
| A、14 | B、21 | C、28 | D、35 |
已知集M={x|y=
},N={x|x=t2,t∈M},则集合M∩N等于( )
| 1-x2 |
| A、M | B、N | C、R | D、ϕ |
已知函数f(x)=
,则f(-7)=( )
|
| A、1 | B、4 | C、16 | D、49 |
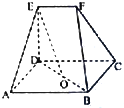 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=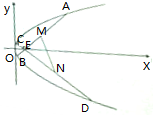 已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点.
已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点. 如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=
如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=