题目内容
复数z满足条件|z-i|+|z+i|=2,那么|z+i+1|的最大值为 ,此时复数z为 .
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:复数z满足条件|z-i|+|z+i|=2,而A(0,1),B(0,-1),线段|AB|=2.可得:复数z表示的点在线段AB上.于是当z=i时,|z+i+1|取得最大值.
解答:
解:∵复数z满足条件|z-i|+|z+i|=2,
而A(0,1),B(0,-1),线段|AB|=2.
∴复数z表示的点在线段AB上.
∴|z+i+1|=|z-(-1-i)|的最大值为
=
,此时z=i.
而A(0,1),B(0,-1),线段|AB|=2.
∴复数z表示的点在线段AB上.
∴|z+i+1|=|z-(-1-i)|的最大值为
| (-1-0)2+(-1-1)2 |
| 5 |
点评:本题考查了复数的几何由于,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
将函数y=
cosx+sinx(x∈R)的图象向左平移m(m>0)个长度单位后,所得到的图象关于原点对称,则m的最小值是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设a,b为实数,则“a>b>0是
<
”的( )
| 1 |
| a |
| 1 |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
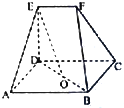 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD= 如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM=
如图,直线l与AB交于点O,点M是AB的中点,过点A、M、B分别作l的垂线,垂足分别是E、F、G.求证:FM= 已知四边形ABCD是边长为1的正方形,MA⊥平面ABCD,MA=2动点P在正方形的边上从点A出发经过点B运动到点C.设点P走过的路程为x,△MAP的面积为S(x),则函数y=S2(x)的图象是( )
已知四边形ABCD是边长为1的正方形,MA⊥平面ABCD,MA=2动点P在正方形的边上从点A出发经过点B运动到点C.设点P走过的路程为x,△MAP的面积为S(x),则函数y=S2(x)的图象是( )


