题目内容
（1）已知tanx=2，求
的值
（2）已知sinx+cosx=
，求sin4x+cos4x的值．
| cosx+sinx |
| cosx-sinx |
（2）已知sinx+cosx=
| 2 |
| 3 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）原式分子分母除以cosx，利用同角三角函数间的基本关系化简，将tanx的值代入计算即可求出值；
（2）已知等式两边平方，利用同角三角函数间基本关系化简求出sinxcosx的值，原式利用完全平方公式变形，将sinxcosx的值代入计算即可求出值．
（2）已知等式两边平方，利用同角三角函数间基本关系化简求出sinxcosx的值，原式利用完全平方公式变形，将sinxcosx的值代入计算即可求出值．
解答：
解：（1）∵tanx=2，
∴原式=
=
=-3；
（2）将已知等式两边平方得：（sinx+cosx）2=1+2sinxcosx=
，即sinxcosx=-
，
则sin4x+cos4x=1-2sin2xcos2x=1-2×
=
．
∴原式=
| 1+tanx |
| 1-tanx |
| 1+2 |
| 1-2 |
（2）将已知等式两边平方得：（sinx+cosx）2=1+2sinxcosx=
| 4 |
| 9 |
| 5 |
| 18 |
则sin4x+cos4x=1-2sin2xcos2x=1-2×
| 25 |
| 18×18 |
| 137 |
| 162 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
曲线f（x）=x3+x-2在点P处的切线与直线x+4y+1=0垂直，则点P的坐标（ ）
| A、（1，0） |
| B、（1，0）或（-1，-4） |
| C、（2，8） |
| D、（2，8）或（-1，-4） |
曲线f（x）=x3+x-2的一条切线平行于直线y=4x-1，则切点P0的坐标为（ ）
| A、（0，-1）或（1，0） |
| B、（1，0）或（-1，-4） |
| C、（-1，-4）或（0，-2） |
| D、（1，0）或（2，8） |
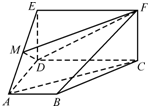如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD=∠CDA=90°，AB=AD=DE=