题目内容
已知△ABC的三个内角A、B、C成等差数列，a、b、c分别为△ABC所对的边．求证：
+
=
（注：可以用分析法证明）
| 1 |
| a+b |
| 1 |
| b+c |
| 3 |
| a+b+c |
考点：综合法与分析法(选修）
专题：选作题,分析法
分析：用分析法证明，结合余弦定理可得结论．
解答：
证明：要证明：
+
=
，
只要证明：
+
=3，
只要证明：
+
=1，
只要证明：c（b+c）+a（a+b）=（a+b）（b+c），
即b2=a2+c2-ac，
∵A、B、C成等差数列，
∴B=60°，
∴由余弦定理，得b2=a2+c2-ac．
∴结论成立．
| 1 |
| a+b |
| 1 |
| b+c |
| 3 |
| a+b+c |
只要证明：
| a+b+c |
| a+b |
| a+b+c |
| b+c |
只要证明：
| c |
| a+b |
| a |
| b+c |
只要证明：c（b+c）+a（a+b）=（a+b）（b+c），
即b2=a2+c2-ac，
∵A、B、C成等差数列，
∴B=60°，
∴由余弦定理，得b2=a2+c2-ac．
∴结论成立．
点评：本题主要考查了等差关系、余弦定理的应用和解三角形问题．考查了学生综合分析问题和基本的运算能力．
练习册系列答案
相关题目
已知函数f（x）=ax3+bx+2013，若f（2014）=4025，则f（-2014）的值为（ ）
| A、1 | B、-4025 |
| C、-2013 | D、2014 |
某小学数学组组织了“自主招生选拔赛”从参加考试的学生中抽出60名学生，将其成绩分为六组[40，50）[50，60），…[90，100]，其部分频率分布直方图如图所示，观察图形，从成绩在[40，50）和[90，100]的学生中随即选两个人，则他们在同一分数段的概率是（ ）
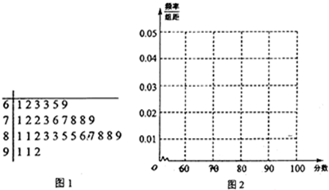
为了了解调研高一年级新学生的智力水平，某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查，测得“智力评分”的频数分布表如表l，表2．