题目内容
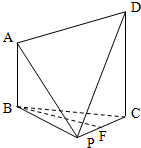 在四棱锥P-ABCD中,AB∥CD,AB=
在四棱锥P-ABCD中,AB∥CD,AB=| 1 |
| 2 |
| 2 |
(Ⅰ)求证:BF∥平面PAD;
(Ⅱ)求证:平面ADP⊥平面PDC;
(Ⅲ)求VP-ABCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取PD的中点为E,连接EF,由已知条件推导出四边形ABFE为平行四边形,由此能证明BF∥平面PAD.
(Ⅱ)由等腰三角形性质得BF⊥PC,由线面垂直得CD⊥平面PBC,从而得到BF⊥平面PDC,由此能证明平面ADP⊥平面PDC.
(Ⅲ)由勾股定理得PB⊥BC,所以PB是四棱锥的高,由此能求出VP-ABCD.
(Ⅱ)由等腰三角形性质得BF⊥PC,由线面垂直得CD⊥平面PBC,从而得到BF⊥平面PDC,由此能证明平面ADP⊥平面PDC.
(Ⅲ)由勾股定理得PB⊥BC,所以PB是四棱锥的高,由此能求出VP-ABCD.
解答:
(Ⅰ)证明:取PD的中点为E,连接EF,
 ∵F为PC中点∴EF为△PDC的中位线,
∵F为PC中点∴EF为△PDC的中位线,
即EF∥DC且EF=
DC.…(2分)
又∵AB∥CD,AB=
CD,∴AB∥EF且AB=EF,
∴四边形ABFE为平行四边形,∴BF∥AE.…(3分)
又∵AE?平面PAD.BF?平面PAD
∴BF∥平面PAD.…(4分)
(Ⅱ)证明:∵BP=BC,F为PC的中点,∴BF⊥PC.…(5分)
又AB⊥平面PBC,AB∥CD,∴CD⊥平面PBC,…(6分)
DC⊥BF,又DC∩PC=C,∴BF⊥平面PDC.…(7分)
由(Ⅰ)知,AE∥BF,
∴AE⊥平面PDC,又AE?平面ADP,
∴平面ADP⊥平面PDC.…(8分)
(Ⅲ)解:∵AB⊥平面PBC,AB?平面ABCD,
∴平面ABCD⊥平面PBC且交线为BC…(9分)
又BP=BC=
,PC=2,∴PB⊥BC,
∴PB⊥平面ABCD,
∴PB是四棱锥的高,…(10分)
∴VP-ABCD=
SABCD•PB=
×(1+2)×
×
×
=1.…(12分)
 ∵F为PC中点∴EF为△PDC的中位线,
∵F为PC中点∴EF为△PDC的中位线,即EF∥DC且EF=
| 1 |
| 2 |
又∵AB∥CD,AB=
| 1 |
| 2 |
∴四边形ABFE为平行四边形,∴BF∥AE.…(3分)
又∵AE?平面PAD.BF?平面PAD
∴BF∥平面PAD.…(4分)
(Ⅱ)证明:∵BP=BC,F为PC的中点,∴BF⊥PC.…(5分)
又AB⊥平面PBC,AB∥CD,∴CD⊥平面PBC,…(6分)
DC⊥BF,又DC∩PC=C,∴BF⊥平面PDC.…(7分)
由(Ⅰ)知,AE∥BF,
∴AE⊥平面PDC,又AE?平面ADP,
∴平面ADP⊥平面PDC.…(8分)
(Ⅲ)解:∵AB⊥平面PBC,AB?平面ABCD,
∴平面ABCD⊥平面PBC且交线为BC…(9分)
又BP=BC=
| 2 |
∴PB⊥平面ABCD,
∴PB是四棱锥的高,…(10分)
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查锥体体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
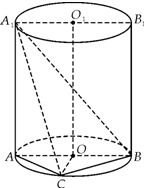 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.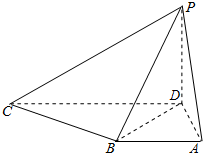 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=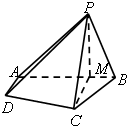 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.