题目内容
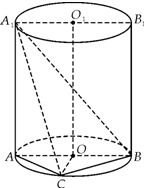 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.(1)求三棱锥A-A1CB的体积;
(2)求异面直线A1B与OC所成的角的大小(结果用反三角函数值表示).
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间角
分析:(1)由题意圆柱OO1的表面积为8π,OA=1,∠AOC=120°建立关于圆柱高的方程求出AA1=3,即得棱锥的高,再由∠AOP=120°解出解出底面积,再棱锥的体积公式求体积即可.
(2)取AA1中点Q,连接OQ,CQ,可得∠COQ或它的补角为异面直线A1B与OC所成的角,在三角形COQ中求异面直线所成的角即可.
(2)取AA1中点Q,连接OQ,CQ,可得∠COQ或它的补角为异面直线A1B与OC所成的角,在三角形COQ中求异面直线所成的角即可.
解答:
解:(1)设AA1=h,∵底面半径R=1,圆柱的表面积为8π,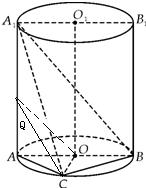
∴2π×12+2πh=8π,解得h=3.
∵点C在底面圆O上,且∠AOC=120°,AB是圆柱OO1底面圆O的直径,
∴AB=2,BC=1,AC=
,∠ACB=90°,
∴S△ACB=
×2×
=
,
∴三棱锥A-A1CB的体积V=
×h×S△ACB=
.
(2)取AA1中点Q,连接OQ,CQ,则OQ∥A1B,
得∠COQ或它的补角为异面直线A1B与OC所成的角.
又AC=
,AQ=
AA1=
,得OQ=
A1B=
=
,
CQ=
=
,OC=1,
由余弦定理得cos∠COQ=
=
=-
,
∴异面直线A1B与OP所成的角为arccos
.

∴2π×12+2πh=8π,解得h=3.
∵点C在底面圆O上,且∠AOC=120°,AB是圆柱OO1底面圆O的直径,
∴AB=2,BC=1,AC=
| 3 |
∴S△ACB=
| 1 |
| 2 |
| 3 |
| 3 |
∴三棱锥A-A1CB的体积V=
| 1 |
| 3 |
| 3 |
(2)取AA1中点Q,连接OQ,CQ,则OQ∥A1B,
得∠COQ或它的补角为异面直线A1B与OC所成的角.
又AC=
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9+4 |
| ||
| 2 |
CQ=
|
| ||
| 2 |
由余弦定理得cos∠COQ=
| CO2+OQ2-CQ2 |
| 2CO•OQ |
1+
| ||||
2×1×
|
| ||
| 13 |
∴异面直线A1B与OP所成的角为arccos
| ||
| 13 |
点评:本题考查了求三棱锥的体积与求两异面直线所成的角,在圆柱这一背景下,考查这两个问题方式比较新颖,解答本题关键是正确理解这些几何图形之间的位置关系的转化.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,E是PC的三等分点,F是PB的中点,求证:AF∥面BDE.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,E是PC的三等分点,F是PB的中点,求证:AF∥面BDE. “交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:
“交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示: 已知函数f(x)=3sin(2x-
已知函数f(x)=3sin(2x- 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点. 在四棱锥P-ABCD中,AB∥CD,AB=
在四棱锥P-ABCD中,AB∥CD,AB=