题目内容
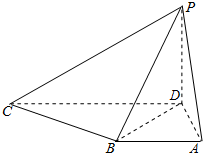 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=| 3 |
(Ⅰ)求证:BC⊥平面PBD;
(Ⅱ)点E是线段PC上的一个动点,二面角E-BA-D的大小是否可以为30°?若可以,求出线段PE的长.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由线面垂直得PD⊥BC,由勾股定理的逆定理得CB⊥BD,由此能证明BC⊥平面PBD.
(Ⅱ)建立空间直角坐标系,利用向量法能求出二面角E-BA-D的大小可以为30°,线段PE的长为
.
(Ⅱ)建立空间直角坐标系,利用向量法能求出二面角E-BA-D的大小可以为30°,线段PE的长为
2
| ||
| 3 |
解答:
 (Ⅰ)证明:∵PD⊥底面ABCD,∴PD⊥BC.…(2分)
(Ⅰ)证明:∵PD⊥底面ABCD,∴PD⊥BC.…(2分)
在直角梯形ABCD中,∠BAD=90°,AB=AD=1,
∴BD=
,BC2=(CD-AB)2+AD2=2,
在△CBD中,由勾股定理的逆定理知,
△CBD是直角三角形,且CB⊥BD.…(4分)
∵PD⊥BC,BC⊥BD,BD∩PD=D,
∴BC⊥平面PBD.…(5分)
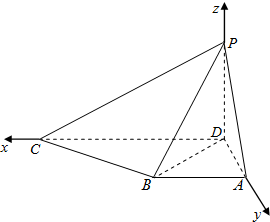
(Ⅱ)解:建立如图所示的空间直角坐标系.
D(0,0,0)、P(0,0,
)、A(0,1,0)、B(1,1,0)、C(2,0,0).…(6分)
平面BAD的一个法向量为
=(0,0,1),…(7分)
设
=λ
(0≤λ≤1),则E(2λ,0,
-
λ),
=(1,0,0),
=(2λ,-1,
-
λ),
设平面EBA的一个法向量为
=(x,y,z),
则
,
取z=1,得
=(0,
-
λ,1),
∵二面角E-BA-D的大小为30°,
∴cos30°=cos<
,
>=
,
解得λ=
,…(10分)
∴|PE|=
λ=
.…(12分)
 (Ⅰ)证明:∵PD⊥底面ABCD,∴PD⊥BC.…(2分)
(Ⅰ)证明:∵PD⊥底面ABCD,∴PD⊥BC.…(2分)在直角梯形ABCD中,∠BAD=90°,AB=AD=1,
∴BD=
| 2 |
在△CBD中,由勾股定理的逆定理知,
△CBD是直角三角形,且CB⊥BD.…(4分)
∵PD⊥BC,BC⊥BD,BD∩PD=D,
∴BC⊥平面PBD.…(5分)
(Ⅱ)解:建立如图所示的空间直角坐标系.
D(0,0,0)、P(0,0,
| 3 |
平面BAD的一个法向量为
| m |
设
| PE |
| PC |
| 3 |
| 3 |
| AB |
| AE |
| 3 |
| 3 |
设平面EBA的一个法向量为
| n |
则
|
取z=1,得
| n |
| 3 |
| 3 |
∵二面角E-BA-D的大小为30°,
∴cos30°=cos<
| n |
| m |
| 1 | ||||||
|
解得λ=
| 2 |
| 3 |
∴|PE|=
| 7 |
2
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查角能否为30°的判断与求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
 “交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:
“交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示: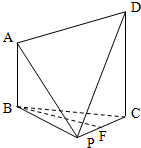 在四棱锥P-ABCD中,AB∥CD,AB=
在四棱锥P-ABCD中,AB∥CD,AB=