题目内容
已知an+1=
,a1=2,求an.
| an-6 |
| an+6 |
考点:数列递推式
专题:等差数列与等比数列
分析:设bn=
,则bn+1=
=
=
=
bn.由此能求出{bn}是首项为
,公比为
的等比数列,从而能求出an.
| an+2 |
| an+3 |
| an+1+2 |
| an+1+3 |
| ||
|
| 3an+6 |
| 4an+12 |
| 3 |
| 4 |
| 4 |
| 5 |
| 3 |
| 4 |
解答:
解:∵an+1=
,a1=2,设bn=
∴bn+1=
=
=
=
bn.
又b1=
=
,
{bn}是首项为
,公比为
的等比数列,
∴bn=
=
•(
)n-1,
解得an=
=
.
| an-6 |
| an+6 |
| an+2 |
| an+3 |
∴bn+1=
| an+1+2 |
| an+1+3 |
| ||
|
| 3an+6 |
| 4an+12 |
| 3 |
| 4 |
又b1=
| a1+2 |
| a1+3 |
| 4 |
| 5 |
{bn}是首项为
| 4 |
| 5 |
| 3 |
| 4 |
∴bn=
| an+2 |
| an+3 |
| 4 |
| 5 |
| 3 |
| 4 |
解得an=
3•
| ||||
2-
|
6•(
| ||
5-2(
|
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
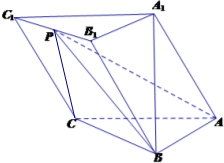 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.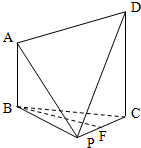 在四棱锥P-ABCD中,AB∥CD,AB=
在四棱锥P-ABCD中,AB∥CD,AB=