题目内容
已知椭圆E：
+
=1（a＞b＞0）的离心率为
，直线l分别经过椭圆长轴和短轴的一个顶点，且与圆C：x2+y2=
相切，
（Ⅰ）求椭圆E的方程；
（Ⅱ）P为圆C上任意一点，以P为切点作圆C的切线与椭圆E相交于点M，N，求线段|MN|的取值范围．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| 3 |
（Ⅰ）求椭圆E的方程；
（Ⅱ）P为圆C上任意一点，以P为切点作圆C的切线与椭圆E相交于点M，N，求线段|MN|的取值范围．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）由已知条件推导出a2=2b2，
=
，由此能求出椭圆E方程．
（Ⅱ）设圆C的切线方程为y=kx+m，则3m2=2-2k2，联立
，得（1+2k2）x2-4kmx+2m2-2=0，由此能求出线段|MN|的取值范围．
| ab | ||
|
| ||
| 3 |
（Ⅱ）设圆C的切线方程为y=kx+m，则3m2=2-2k2，联立
|
解答：
解：（Ⅰ）∵椭圆E：
+
=1（a＞b＞0）的离心率为
，
∴a2=2b2，
不妨设l：
+
=1，即bx+ay-ab=0，
则
=
，
解得a=
，b=1，
∴椭圆E方程为：
+y2=1．
（Ⅱ）设圆C的切线方程为y=kx+m，
∴
=
，整理，得3m2=2-2k2，
联立
，得（1+2k2）x2-4kmx+2m2-2=0，
△＞0，设M（x1，y1），N（x2，y2），
则x1+x2=
，x1x2=
，
∴|MN|=
|x1-x2|=
•
=
•
，
令1+2k2=t≥1，
则|MN|2=
=
•
=
[-(
)2+(
)+2]，
又0＜
≤1，∴当
=
时，
即k2=
时，|MN|max=
．
＞0时，|MN|＞
，
∴线段|MN|的取值范围是（
，
]．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴a2=2b2，
不妨设l：
| x |
| a |
| y |
| b |
则
| ab | ||
|
| ||
| 3 |
解得a=
| 2 |
∴椭圆E方程为：
| x2 |
| 2 |
（Ⅱ）设圆C的切线方程为y=kx+m，
∴
| m | ||
|
| ||
| 3 |
联立
|
△＞0，设M（x1，y1），N（x2，y2），
则x1+x2=
| 4km |
| 1+2k2 |
| 2m2-2 |
| 1+2k2 |
∴|MN|=
| 1+k2 |
| 1+k2 |
| ||
| 1+2k2 |
| 1+k2 |
| ||||
| 1+2k2 |
令1+2k2=t≥1，
则|MN|2=
| ||||
| t2 |
| 4 |
| 3 |
| 2t2+t-1 |
| t2 |
| 4 |
| 3 |
| 1 |
| t |
| 1 |
| t |
又0＜
| 1 |
| t |
| 1 |
| t |
| 1 |
| 2 |
即k2=
| 1 |
| 2 |
| 3 |
| 1 |
| t |
2
| ||
| 3 |
∴线段|MN|的取值范围是（
2
| ||
| 3 |
| 3 |
点评：本题考查椭圆方程的求法，考查线段长的取值范围的求法，解题时要认真审题，注意椭圆弦长公式的合理运用．
练习册系列答案
相关题目
在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M，N分别是AB，PC的中点．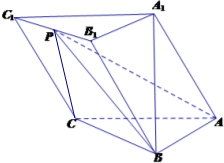
如图，在三棱柱ABC-A1B1C1中，AB⊥AC，顶点A1在底面ABC上的射影恰为点B，且AB=AC=A1B=2．
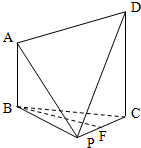在四棱锥P-ABCD中，AB∥CD，AB=
如图，正方体ABCD-A1B1C1D1的棱长为1，E是A1B1的中点，则下列四个命题：