题目内容
数列{an}满足条件a1=1,an=an-1+(
)n-1(n=2,3,…).
(1)求{an};
(2)求a1+a2+a3+…+an.
| 1 |
| 3 |
(1)求{an};
(2)求a1+a2+a3+…+an.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由已知得a1=1,an-an-1=(
)n-1,由此利用累加法能求出an.
(2)由an=
-
,利用分组求和法能求出a1+a2+a3+…+an.
| 1 |
| 3 |
(2)由an=
| 3 |
| 2 |
| 1 |
| 2•3n-1 |
解答:
解:(1)∵数列{an}满足条件a1=1,an=an-1+(
)n-1(n=2,3,…),
∴an-an-1=(
)n-1,
∴an=a1+a2-a1+a3-a2+…+an-an-1
=1+
+(
)2+…+(
)n-1
=
=
-
.
(2)a1+a2+a3+…+an
=
n-
[1+
+(
)2+…+(
)n-1]
=
n-
×
=
n-
-
.
| 1 |
| 3 |
∴an-an-1=(
| 1 |
| 3 |
∴an=a1+a2-a1+a3-a2+…+an-an-1
=1+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
1-
| ||
1-
|
| 3 |
| 2 |
| 1 |
| 2•3n-1 |
(2)a1+a2+a3+…+an
=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 3 |
| 2 |
| 1 |
| 2 |
1-
| ||
1-
|
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4•3n-1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意累加法和分组求和法的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
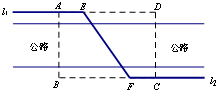 如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=