题目内容
给出下列五个命题:
①函数y=tanx的图象关于点(kπ+
,0)(k∈Z)对称;
②函数f(x)=tanx是最小正周期为π的周期函数;
③函数y=cos2x+sinx的最小值为-1;
④设θ为第二象限的角,则tan
>cos
,且sin
>cos
;
⑤若θ第三象限角,则点P(sin(cosθ),cos(cosθ))在第二象限.
其中正确的命题序号是 ..
①函数y=tanx的图象关于点(kπ+
| π |
| 2 |
②函数f(x)=tanx是最小正周期为π的周期函数;
③函数y=cos2x+sinx的最小值为-1;
④设θ为第二象限的角,则tan
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
⑤若θ第三象限角,则点P(sin(cosθ),cos(cosθ))在第二象限.
其中正确的命题序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:对于①,正切函数y=tanx的对称中心为图象与x轴的交点以及其渐近线与x轴的交点,依此判断;
对于②,由正切函数的性质可知②是正确的;
对于③,先化成y=--sin2x+sinx+1=-(sinx-
)2+
≥-(-1-
)2+
=-1,则结论可以确定;
对于④,根据θ的范围,可知
的范围是(kπ+
,kπ+
),k∈Z,据此可以判断两个不等式的对错;
对于⑤,因为θ是第三象限的角,所以-1<cosθ<0,而(-1,0)⊆(-
,0),据此判断sin(cosθ)与cos(cosθ)的符号.
对于②,由正切函数的性质可知②是正确的;
对于③,先化成y=--sin2x+sinx+1=-(sinx-
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
对于④,根据θ的范围,可知
| θ |
| 2 |
| π |
| 4 |
| π |
| 2 |
对于⑤,因为θ是第三象限的角,所以-1<cosθ<0,而(-1,0)⊆(-
| π |
| 2 |
解答:
解:对于①,函数y=tanx的图象的对称中心为(
,0)?(kπ+
,0)(k∈Z),故①正确;
对于②,由正切函数的性质可知②是正确的;
对于③,先将原函数化成y=-sin2x+sinx+1=-(sinx-
)2+
≥-(-1-
)2+
=-1,故③是正确的;
对于④,根据θ的范围,可知
的范围是(kπ+
,kπ+
),k∈Z,当k是奇数时,则有0>cos
>sin
>-1,故④错误;
对于⑤,因为θ是第三象限的角,所以-1<cosθ<0,而(-1,0)⊆(-
,0),所以sin(cosθ)<0,cos(cosθ)>0,所以点P(sin(cosθ),cos(cosθ))在第二象限,故⑤正确.
故答案为:①②③⑤
| kπ |
| 2 |
| π |
| 2 |
对于②,由正切函数的性质可知②是正确的;
对于③,先将原函数化成y=-sin2x+sinx+1=-(sinx-
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
对于④,根据θ的范围,可知
| θ |
| 2 |
| π |
| 4 |
| π |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
对于⑤,因为θ是第三象限的角,所以-1<cosθ<0,而(-1,0)⊆(-
| π |
| 2 |
故答案为:①②③⑤
点评:本题以命题考查为载体考查三角函数的有关知识和方法,属于基础题,难度不大.

练习册系列答案
相关题目
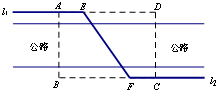 如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=