题目内容
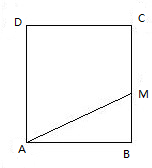 已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.
已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:分别讨论M点在B,C之间,C,D之间,D,A之间的x的取值,根据三角形面积公式求出每种情况下的面积即可.
解答:
解:当点M在B,C之间时,即x∈[0,2),S=
•2x=x;
当点M在C,D之间时,即x∈[2,4),S=2;
当点M在D,A之间时,即x∈[4,6],S=
•2•(6-x)=6-x;
∴S=
,该函数的定义域为[0,6].
| 1 |
| 2 |
当点M在C,D之间时,即x∈[2,4),S=2;
当点M在D,A之间时,即x∈[4,6],S=
| 1 |
| 2 |
∴S=
|
点评:考查函数的解析式,以及根据实际问题求解析式的方法,分段函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|x>4或x<-1},B={x|ax-1>0},若A∪B=A,则实数a的取值范围是( )
A、(0,
| ||
B、(-1,0)∪(0,
| ||
C、(-1,
| ||
D、[-1,
|
已知a、b是不相等的正数,且a、x、y、b成等差数列,a、m、n、b成等比数列,则下列关系成立的是( )
| A、x+y>m+n |
| B、x+y=m+n |
| C、x+y<m+n |
| D、不能确定 |
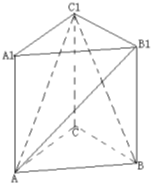 (文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.