题目内容
已知△ABC是边长为2的正三角形,则它的平面直观图△A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面图形的直观图
专题:计算题,空间位置关系与距离
分析:求出三角形的面积,利用平面图形的面积是直观图面积的2
倍,求出直观图的面积即可
| 2 |
解答:
解:由三角形ABC是边长为2的正三角形,
知三角形ABC的面积为:S=
×2×2×sin60°=
;
因为平面图形的面积与直观图的面积的比是2
,
所以它的平面直观图的面积是:
=
.
故选:C.
知三角形ABC的面积为:S=
| 1 |
| 2 |
| 3 |
因为平面图形的面积与直观图的面积的比是2
| 2 |
所以它的平面直观图的面积是:
| ||
2
|
| ||
| 4 |
故选:C.
点评:本题是基础题,考查平面图形与直观图的面积的求法,考查二者的关系,考查计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
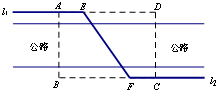 如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=