题目内容
已知f(x)=log2(1-x).
(1)求f(x)的定义域;
(2)求使f(x)>0成立的x的取值范围.
(1)求f(x)的定义域;
(2)求使f(x)>0成立的x的取值范围.
考点:对数函数的值域与最值,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)通过对数函数真数大于0求得函数的定义域.
(2)根据对数函数的单调性确定关于x的不等式求得x的范围.
(2)根据对数函数的单调性确定关于x的不等式求得x的范围.
解答:
解:(1)要使函数有意义,需1-x>0,即x<1,
∴函数的定义域为(-∞,1).
(2)∵函数y=log2(1-x)为单调递增函数,log21=0,
∴f(x)>0成立时,1-x>1,x<0,
综合函数的定义域得x的范围为x<0.
∴函数的定义域为(-∞,1).
(2)∵函数y=log2(1-x)为单调递增函数,log21=0,
∴f(x)>0成立时,1-x>1,x<0,
综合函数的定义域得x的范围为x<0.
点评:本题主要考查了对数函数的性质.考查了学生对对数函数基础知识的掌握.

练习册系列答案
相关题目
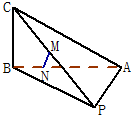 已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.
已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.