题目内容
计算
xdx= .
| ∫ | 1 -1 |
考点:定积分
专题:导数的综合应用
分析:根据
x2的导数等于x,得到原函数是
x2,写出当自变量取两个不同的值时,对应的函数值,让两个数字相减得到结果.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∫12xdx=
x2
=
×12-
×12=0.
故答案为:0.
| 1 |
| 2 |
| | | 1 -1 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:0.
点评:本题考查定积分,本题解题的关键是写出要积分的函数的原函数,本题是一个基础题,若出现一定是一个送分题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
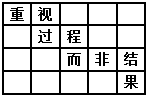 将“重视过程而非结果”8个汉字填入5*4的方格内,其中“重”字填入左上角,“果”字填入右下角,将其余6个汉字依次填入方格,要求只能向右或向下读成一句原话,如图所示为一种填法,则共有
将“重视过程而非结果”8个汉字填入5*4的方格内,其中“重”字填入左上角,“果”字填入右下角,将其余6个汉字依次填入方格,要求只能向右或向下读成一句原话,如图所示为一种填法,则共有