题目内容
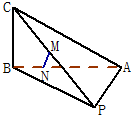 已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.
已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.(1)求证明:MN⊥AB;
(2)当∠APB=90°,BC=2,AB=4时,求MN的长.
考点:直线与平面垂直的性质,点、线、面间的距离计算
专题:空间位置关系与距离
分析:证明直线与直线垂直可将其中一条直线放到平面内,平面的选择可借助题目中已知的一些垂直关系取寻找,有中点的问题可利用中位线性质解决
解答:
(1)证明:如图:
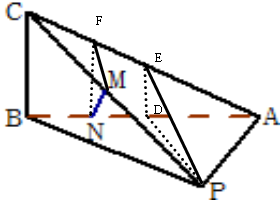
取AB,AC的中点分别为D、E,
取BD、EC的中点分别为N、F,
连接PD、PE、DE、MF、NF,
由PA=PB知PD⊥AB,D、E为直线AB,AC的中点,DE∥BC,而BC⊥平面PAB,
∴DE⊥AB,而PD∩DE=D,
∴AB⊥平面PDE,而NF∥DE,MF∥PE 知平面PDE∥平面MNF,
∴AB⊥平面MNF,MN?平面MNF,
∴MN⊥AB.
(2)解:由(1)以及BC=2可得GM=1,
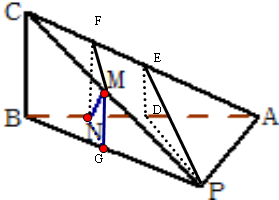
取BP中点为G,则MG∥BC,又BC⊥面ABP,
∴MG⊥面ABP,
∴MG⊥GN,
GN=
PD=
AB=1,
∴MN=
=
.

取AB,AC的中点分别为D、E,
取BD、EC的中点分别为N、F,
连接PD、PE、DE、MF、NF,
由PA=PB知PD⊥AB,D、E为直线AB,AC的中点,DE∥BC,而BC⊥平面PAB,
∴DE⊥AB,而PD∩DE=D,
∴AB⊥平面PDE,而NF∥DE,MF∥PE 知平面PDE∥平面MNF,
∴AB⊥平面MNF,MN?平面MNF,
∴MN⊥AB.
(2)解:由(1)以及BC=2可得GM=1,

取BP中点为G,则MG∥BC,又BC⊥面ABP,
∴MG⊥面ABP,
∴MG⊥GN,
GN=
| 1 |
| 2 |
| 1 |
| 4 |
∴MN=
| GM2+GN2 |
| 2 |
点评:本题主要考查了直线与直线的位置关系,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
相关题目

 某食品厂为.检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),作出样本的频率分布直方图如图所示.
某食品厂为.检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),作出样本的频率分布直方图如图所示.