题目内容
已知二次函数h(x)=ax2+3x+c(c>3),其中函数h′(x)的零点为
,f(x)=lnx-h(x)
(1)若函数f(x)在(
,m+
)上为单调函数,求m的范围
(2)若函数y=2x-lnx,x∈[1,4]的图象总在y=f(x)图象上方,求c的取值范围.
| 3 |
| 2 |
(1)若函数f(x)在(
| 1 |
| 2 |
| 1 |
| 4 |
(2)若函数y=2x-lnx,x∈[1,4]的图象总在y=f(x)图象上方,求c的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(1)由h′(x)的零点为
,得h′(
)=0,可求a,由函数f(x)在(
,m+
)上为单调函数,知f′(x)≥0,或f′(x)≤0在(
,m+
)上恒成立,利用二次函数的性质可得
<m+
≤1,解出即可;
(2)由函数y=2x-lnx,x∈[1,4]的图象总在y=f(x)图象上方,可得2x-lnx>f(x),即5x-x2-2lnx+c>0在∈[1,4]上恒成立,令g(x)=5x-x2-2lnx+c,x∈[1,4],利用导数可求得g(x)min,从而有g(x)min>0,解出可得;
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)由函数y=2x-lnx,x∈[1,4]的图象总在y=f(x)图象上方,可得2x-lnx>f(x),即5x-x2-2lnx+c>0在∈[1,4]上恒成立,令g(x)=5x-x2-2lnx+c,x∈[1,4],利用导数可求得g(x)min,从而有g(x)min>0,解出可得;
解答:
解:(1)h′(x)=2ax+3,
∵h′(x)的零点为
,
∴h′(
)=2a×
+3=0,解得a=-1,
则f(x)=lnx-h(x)=lnx+x2-3x-c,
f′(x)=
+2x-3=
,
令f′(x)=0,得x=
或1,
∵y=2x2-3x+1的图象开口向上,且函数f(x)在(
,m+
)上为单调函数,
∴
<m+
≤1,解得
<m≤
,
故实数m的取值范围是(
,
].
(2)∵函数y=2x-lnx,x∈[1,4]的图象总在y=f(x)图象上方,
∴2x-lnx>f(x),即5x-x2-2lnx+c>0在∈[1,4]上恒成立,
令g(x)=5x-x2-2lnx+c,x∈[1,4],
则g′(x)=5-2x-
=-
,
当x∈[1,2)时,g′(x)>0,g(x)递增;当x∈(2,4]时,g′(x)<0,g(x)递减,
∴g(x)min=min{g(1),g(4)},
又g(1)=4+c,g(4)=4-2ln4+c,g(1)>g(4),
∴g(x)min=g(4)=4-2ln4+c,
∴4-2ln4+c>0,解得c>2ln4-4,
∴c的取值范围是(2ln4-4,+∞).
∵h′(x)的零点为
| 3 |
| 2 |
∴h′(
| 3 |
| 2 |
| 3 |
| 2 |
则f(x)=lnx-h(x)=lnx+x2-3x-c,
f′(x)=
| 1 |
| x |
| 2x2-3x+1 |
| x |
令f′(x)=0,得x=
| 1 |
| 2 |
∵y=2x2-3x+1的图象开口向上,且函数f(x)在(
| 1 |
| 2 |
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
故实数m的取值范围是(
| 1 |
| 4 |
| 3 |
| 4 |
(2)∵函数y=2x-lnx,x∈[1,4]的图象总在y=f(x)图象上方,
∴2x-lnx>f(x),即5x-x2-2lnx+c>0在∈[1,4]上恒成立,
令g(x)=5x-x2-2lnx+c,x∈[1,4],
则g′(x)=5-2x-
| 2 |
| x |
2(x-
| ||
| x |
当x∈[1,2)时,g′(x)>0,g(x)递增;当x∈(2,4]时,g′(x)<0,g(x)递减,
∴g(x)min=min{g(1),g(4)},
又g(1)=4+c,g(4)=4-2ln4+c,g(1)>g(4),
∴g(x)min=g(4)=4-2ln4+c,
∴4-2ln4+c>0,解得c>2ln4-4,
∴c的取值范围是(2ln4-4,+∞).
点评:本题以函数为载体,考查利用导数研究函数的单调性、最值及函数恒成立问题,考查转化思想,考查学生解决问题的能力.

练习册系列答案
相关题目
已知命题p:若非零实数a,b,则
<
;命题q:对任意实数x∈(0,+∞),log
(x+1)<0,则下列命题为真命题的是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| A、p且q | B、p或¬q |
| C、¬p且q | D、p且¬q |
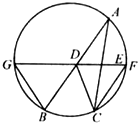 如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明: