题目内容
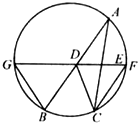 如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明:(Ⅰ)CF∥AB;
(Ⅱ)△BCD∽△GBD.
考点:相似三角形的判定,平行线分线段成比例定理
专题:立体几何
分析:(I)如图所示,利用三角形的中位线定理和平行四边形的性质即可证明;
(II)利用平行线的性质、平行四边形的性质、圆的性质、相似三角形的判定定理即可得出.
(II)利用平行线的性质、平行四边形的性质、圆的性质、相似三角形的判定定理即可得出.
解答:
证明:(I)如图所示,
∵D,E分别为△ABC边AB,AC的中点,
∴DE
BC,
又BC=2EF,
∴DE=EF.
∴四边形ADCF是平行四边形,
∴CF∥AB.
(II)∵CF∥AB,∴BC=AF.
由四边形ADCF是平行四边形,∴CD=AF.∴CD=CB,∴∠CBD=∠CDB.∵FG∥BC,∴∠BGD=∠CFD.
∵CF∥AB,∴∠BDG=∠CFD.
∴∠CBD=∠BDG=∠CDB=∠DGB.
∴△BCD∽△DBG.

∵D,E分别为△ABC边AB,AC的中点,
∴DE
| ∥ |
. |
| 1 |
| 2 |
又BC=2EF,
∴DE=EF.
∴四边形ADCF是平行四边形,
∴CF∥AB.
(II)∵CF∥AB,∴BC=AF.
由四边形ADCF是平行四边形,∴CD=AF.∴CD=CB,∴∠CBD=∠CDB.∵FG∥BC,∴∠BGD=∠CFD.
∵CF∥AB,∴∠BDG=∠CFD.
∴∠CBD=∠BDG=∠CDB=∠DGB.
∴△BCD∽△DBG.
点评:本题考查了三角形的中位线定理和平行四边形的性质、平行四边形的性质、圆的性质、相似三角形的判定定理,考查了推理能力,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
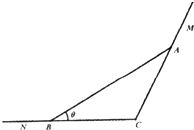 如图,用木板AB借助墙角MCN转成一个三角形ABC区域,用以堆放谷物,已知∠MCN=
如图,用木板AB借助墙角MCN转成一个三角形ABC区域,用以堆放谷物,已知∠MCN=