题目内容
已知函数f(x)=alnx+
+
,a∈R.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(x-1)(e-x-x)+2lnx<
.
| 1 |
| x |
| 1 |
| 2x2 |
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(x-1)(e-x-x)+2lnx<
| 2 |
| 3 |
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:第(Ⅰ)问对函数f(x)求导,导数是含有参数a的表达式,要按a进行分类讨论;
第(Ⅱ)问利用导数证明不等式,要转化成函数求最值问题解决,利用放缩法进行证明.
第(Ⅱ)问利用导数证明不等式,要转化成函数求最值问题解决,利用放缩法进行证明.
解答:
解:(Ⅰ)f(x)的定义域为(0,+∞),f′(x)=
-
-
=
…2分
当a≤0时,f′(x)<0,则f(x)在(0,+∞)内单调递减;…4分
当a>0时,x∈(0,
),f′(x)<0,f(x)单调递减;
x∈(
,+∞),f′(x)>0,f(x)单调递增;…6分
(Ⅱ)当a=2时,由(1)可知f(x)在(0,1)内单调递减,在(1,+∞)内单调递增,
∴f(x)max=f(1)=
,2lnx+
+
≥
…8分
即2ln
+x+
≥
,∴2lnx-x-
≤-
∵(x-1)(e-x-x)+2lnx=(x-1)e-x-x2+x+2lnx
=(x-1)e-x-
+2x+(2lnx-x-
)
<(x-1)e-x-
+2x-
令g(x)=(x-1)e-x-
+2x,x>0
而g′(x)=(2-x)(e-x+1),可知x=2时,g(x)取得最大值,即g(x)≤g(2)=
+2…10分
∴(x-1)e-x-
+2x+2lnx-x-
=2lnx+(x-1)(e-x-x)<
+2-
<
…12分
| a |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
| ax2-x-1 |
| x3 |
当a≤0时,f′(x)<0,则f(x)在(0,+∞)内单调递减;…4分
当a>0时,x∈(0,
1+
| ||
| 2a |
x∈(
1+
| ||
| 2a |
(Ⅱ)当a=2时,由(1)可知f(x)在(0,1)内单调递减,在(1,+∞)内单调递增,
∴f(x)max=f(1)=
| 3 |
| 2 |
| 1 |
| x |
| 1 |
| 2x2 |
| 3 |
| 2 |
即2ln
| 1 |
| x |
| x2 |
| 2 |
| 3 |
| 2 |
| x2 |
| 2 |
| 3 |
| 2 |
∵(x-1)(e-x-x)+2lnx=(x-1)e-x-x2+x+2lnx
=(x-1)e-x-
| x2 |
| 2 |
| x2 |
| 2 |
<(x-1)e-x-
| x2 |
| 2 |
| 3 |
| 2 |
令g(x)=(x-1)e-x-
| x2 |
| 2 |
而g′(x)=(2-x)(e-x+1),可知x=2时,g(x)取得最大值,即g(x)≤g(2)=
| 1 |
| e2 |
∴(x-1)e-x-
| x2 |
| 2 |
| x2 |
| 2 |
| 1 |
| e2 |
| 3 |
| 2 |
| 2 |
| 3 |
点评:本题是导数的综合应用问题,利用导数研究函数的单调性及求函数的最值;考查了分类讨论、转化的思想及放缩法证明不等式.

练习册系列答案
相关题目
函数f(x)=ax2-ax+1(a≠0),如果f(-k)<0,则f(k+1)的值是( )
| A、正数 | B、负数 | C、零 | D、无法确定 |
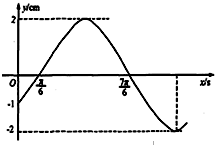 如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-
如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-